Basic Problem: Start with assumptions about ![]() or CDF of random
vector
or CDF of random
vector
![]() . Define
. Define
![]() to be some function
of
to be some function
of ![]() (usually some statistic of interest). How can we compute the distribution
or CDF or density of
(usually some statistic of interest). How can we compute the distribution
or CDF or density of ![]() ?
?
Univariate Techniques
Method 1: compute the CDF by integration and differentiate to find ![]() .
.
Example:
![]() Uniform
Uniform![]() and
and ![]() .
.
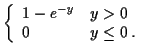 |
Example:
![]() , i.e.
, i.e.
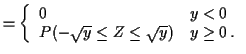 |
![$\displaystyle f_Y(y) = \left\{ \begin{array}{ll}
0 & y < 0
\\
\frac{d}{dy}\le...
...(-\sqrt{y})\right] & y > 0
\\
\mbox{undefined} & y=0 \, .
\end{array}\right.
$](img21.gif)
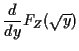 |
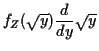 |
||
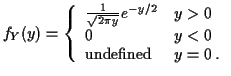
We will find indicator notation useful:
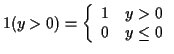
Notice: I never evaluated ![]() before differentiating it. In fact
before differentiating it. In fact
![]() and
and ![]() are integrals I can't do but I can differentiate then anyway.
Remember fundamental theorem of calculus:
are integrals I can't do but I can differentiate then anyway.
Remember fundamental theorem of calculus:
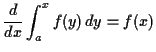
Summary: for ![]() with
with ![]() and
and ![]() each real valued
each real valued
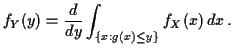
Method 2: Change of variables.
Assume ![]() is one to one.
I do:
is one to one.
I do: ![]() is increasing and differentiable.
Interpretation of density (based on density =
is increasing and differentiable.
Interpretation of density (based on density = ![]() ):
):
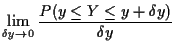 |
|||
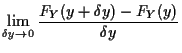 |
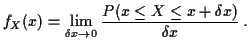
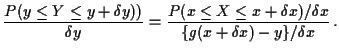
Alternative view:
Each probability is integral of a density.
The first is the
integral of the density of ![]() over the small interval from
over the small interval from ![]() to
to
![]() . The interval is narrow so
. The interval is narrow so ![]() is
nearly constant and
is
nearly constant and
Remark: For ![]() decreasing
decreasing
![]() but Then
the interval
but Then
the interval
![]() is really
is really
![]() so
that
so
that
![]() .
In both cases this amounts to the formula
.
In both cases this amounts to the formula
Mnemonic:
Example:
![]() Weibull(shape
Weibull(shape ![]() , scale
, scale ![]() )
or
)
or
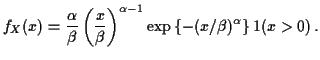
Let ![]() or
or
![]() .
.
Solve ![]() :
:
![]() or
or
![]() .
.
Then
![]() and
and
![]() .
.
Hence
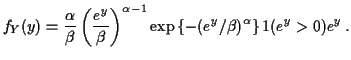
Simplest multivariate problem:
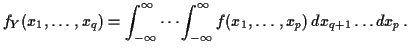
![]() is the marginal density of
is the marginal density of
![]() and
and ![]() the joint density of
the joint density of ![]() but
they are both just densities.
``Marginal'' just to
distinguish from the joint density of
but
they are both just densities.
``Marginal'' just to
distinguish from the joint density of ![]() .
.
Example The function
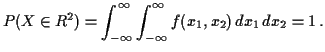
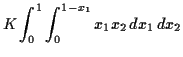 |
|
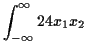 |
||
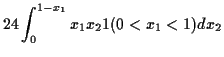 |
||
General problem has
![]() with
with
![]() .
.
Case 1: ![]() .
. ![]() won't have density
for ``smooth''
won't have density
for ``smooth'' ![]() .
. ![]() will have a singular or discrete distribution.
Problem rarely of real interest.
(But, e.g., residuals have singular distribution.)
will have a singular or discrete distribution.
Problem rarely of real interest.
(But, e.g., residuals have singular distribution.)
Case 2: ![]() . We use a
change of variables
formula which generalizes the one derived above for the
case
. We use a
change of variables
formula which generalizes the one derived above for the
case ![]() . (See below.)
. (See below.)
Case 3: ![]() .
Pad out
.
Pad out ![]() -add on
-add on ![]() more variables (carefully chosen)
say
more variables (carefully chosen)
say
![]() . Find functions
. Find functions
![]() . Define for
. Define for ![]() ,
,
![]() and
and
![]() Choose
Choose ![]() so that we can use change of variables on
so that we can use change of variables on
![]() to compute
to compute ![]() . Find
. Find ![]() by integration:
by integration:
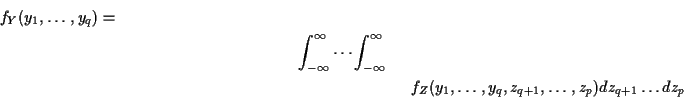
Suppose
![]() with
with ![]() having density
having density ![]() .
Assume
.
Assume ![]() is a one to one (``injective") map, i.e.,
is a one to one (``injective") map, i.e.,
![]() if and only if
if and only if ![]() .
Find
.
Find ![]() :
:
Step 1: Solve for ![]() in terms of
in terms of ![]() :
:
![]() .
.
Step 2: Use basic equation:
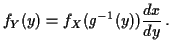
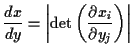
Equivalent formula inverts the matrix:
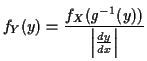
![$\displaystyle \left\vert\frac{dy}{dx}\right\vert =
\left\vert \mbox{det} \left...
...} & \cdots &
\frac{\partial y_p}{\partial x_p}
\end{array} \right]\right\vert
$](img137.gif)
Example: The density
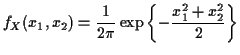
Solve for ![]() in terms of
in terms of ![]() :
:
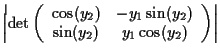 |
|||
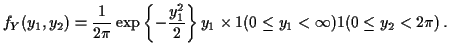
Next: marginal densities of ![]() ,
, ![]() ?
?
Factor ![]() as
as
![]() where
where
Then
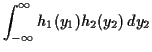 |
|||
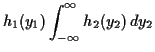 |
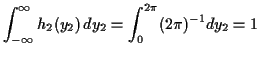
Exercise: ![]() has standard exponential
distribution.
has standard exponential
distribution.
Recall: by definition ![]() has a
has a
![]() distribution on 2 degrees of freedom.
distribution on 2 degrees of freedom.
Exercise: find ![]() density.
density.
Note: We show below factorization of density is equivalent to independence.