


Postscript version of this page
STAT 801: Mathematical Statistics
Independence, conditional distributions
So far density of  specified
explicitly. Often modelling
leads to a specification in terms of marginal and conditional
distributions.
specified
explicitly. Often modelling
leads to a specification in terms of marginal and conditional
distributions.
Def'n: Events 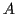 and
and 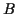 are independent if
are independent if
(Notation: 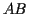 is the event that both
is the event that both 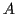 and
and 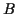 happen,
also written
happen,
also written  .)
.)
Def'n:  ,
,
 are
independent if
are
independent if
for any
 .
.
Example: 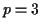
All these equations needed for independence!
Example: Toss a coin twice.
 |
 first toss is a Head first toss is a Head |
|
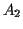 |
 second toss is a Head second toss is a Head |
|
 |
 first toss and second toss different first toss and second toss different |
|
Then
 for each
for each  and for
and for 
but
Def'n:  and
and  are
independent if
are
independent if
for all 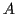 and
and 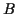 .
.
Def'n: Rvs
 independent:
independent:
for any
 .
.
Theorem:
- If
 and
and  are independent then for all
are independent then for all 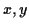
- If
 and
and  are independent with joint density
are independent with joint density
 then
then  and
and  have densities
have densities  and
and  ,
and
,
and
- If
 and
and  independent with marginal densities
independent with marginal densities
 and
and  then
then  has joint density
has joint density
- If
 for all
for all 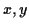 then
then  and
and  are independent.
are independent.
- If
 has density
has density  and there exist
and there exist
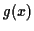 and
and  st
st
 for (almost) all
for (almost) all  then
then
 and
and  are independent with densities
given by
are independent with densities
given by
Proof:
- Since
 and
and  are independent so are the events
are independent so are the events
 and
and  ; hence
; hence
- Suppose
 and
and  real valued.
real valued.
Asst 2: existence of  implies that of
implies that of  and
and  (marginal density formula).
Then for any sets
(marginal density formula).
Then for any sets 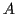 and
and 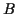
Since
 It follows (measure theory) that the quantity in [] is 0
(almost every pair
It follows (measure theory) that the quantity in [] is 0
(almost every pair  ).
).
- For any
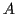 and
and 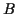 we have
we have
If we define
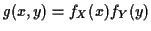 then we have proved that
for
then we have proved that
for
 To prove that
To prove that 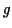 is
is  we need only
prove that this integral formula is valid for an arbitrary Borel set
we need only
prove that this integral formula is valid for an arbitrary Borel set
 , not just a rectangle
, not just a rectangle
 .
.
This is proved via a
monotone class argument. The collection of sets  for which identity holds has closure properties which guarantee that
this collection includes the Borel sets.
for which identity holds has closure properties which guarantee that
this collection includes the Borel sets.
- Another monotone class argument.
-
Take  to see that
where
to see that
where
 .
So
.
So 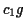 is the density of
is the density of  .
Since
.
Since
 we see that
we see that
 so that
so that
 . Similar argument for
. Similar argument for  .
.
Theorem: If
 are independent and
are independent and
 then
then
 are independent.
Moreover,
are independent.
Moreover,
 and
and
 are
independent.
are
independent.
Conditional probability
Def'n:
 if
if
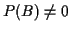 .
.
Def'n: For discrete  and
and  the conditional
probability mass function of
the conditional
probability mass function of  given
given  is
is
For absolutely continuous 
 for all
for all
 . What is
. What is  or
or
 ?
Solution: use limit
?
Solution: use limit
If, e.g.,  have joint density
have joint density  then with
then with
 we have
we have
Divide top, bottom by 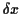 ; let
; let
 .
Denom converges to
.
Denom converges to  ; numerator converges to
Define conditional cdf of
; numerator converges to
Define conditional cdf of  given
given  :
Differentiate wrt
:
Differentiate wrt  to get def'n of
conditional density of
to get def'n of
conditional density of  given
given  :
in words ``conditional = joint/marginal''.
:
in words ``conditional = joint/marginal''.



Richard Lockhart
2001-01-05
![]() specified
explicitly. Often modelling
leads to a specification in terms of marginal and conditional
distributions.
specified
explicitly. Often modelling
leads to a specification in terms of marginal and conditional
distributions.
![]() and
and ![]() are independent if
are independent if
![]() ,
,
![]() are
independent if
are
independent if
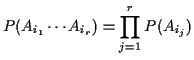
![]()
![]() for each
for each ![]() and for
and for ![]()
![]() and
and ![]() are
independent if
are
independent if
![]() independent:
independent:


![]() implies that of
implies that of ![]() and
and ![]() (marginal density formula).
Then for any sets
(marginal density formula).
Then for any sets ![]() and
and ![]()



![$\displaystyle \int_A\int_B [ f_{X,Y}(x,y) - f_X(x)f_Y(y) ]dydx = 0 \, .
$](img61.gif)



![]() for which identity holds has closure properties which guarantee that
this collection includes the Borel sets.
for which identity holds has closure properties which guarantee that
this collection includes the Borel sets.



![]() if
if
![]() .
.
![]() and
and ![]() the conditional
probability mass function of
the conditional
probability mass function of ![]() given
given ![]() is
is
![]()
![]() for all
for all
![]() . What is
. What is ![]() or
or
![]() ?
Solution: use limit
?
Solution: use limit



