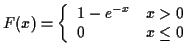Probability Space (or Sample Space): ordered
triple
![]() .
.
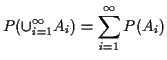
Axioms guarantee can compute probabilities by usual rules, including approximation.
Consequences of axioms:
Vector valued random variable: function
![]() such that,
writing
such that,
writing
![]() ,
,
In almost all of probability and statistics the dependence of a random variable on
a point in the probability space is hidden! You almost always see ![]() not
not ![]() .
.
Borel ![]() -field in
-field in ![]() : smallest
: smallest ![]() -field in
-field in ![]() containing every open ball.
containing every open ball.
Every common set is a Borel set, that is, in the Borel ![]() -field.
-field.
An ![]() valued random variable is a map
valued random variable is a map
![]() such that
when
such that
when ![]() is Borel then
is Borel then
![]() .
.
Fact: this is equivalent to
Jargon and notation: we write ![]() for
for
![]() and define the distribution of
and define the distribution of ![]() to be the map
to be the map
Cumulative Distribution Function (CDF) of ![]() : function
: function ![]() on
on ![]() defined by
defined by
The distribution of a random variable ![]() is discrete
(we also call the random variable discrete) if there
is a countable set
is discrete
(we also call the random variable discrete) if there
is a countable set
![]() such that
such that
Distribution of rv ![]() is absolutely continuous
if there is a function
is absolutely continuous
if there is a function ![]() such that
such that
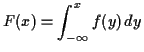
For most values of ![]() we then have
we then have
![]() is differentiable at
is differentiable at ![]() and
and
Example: ![]() is Uniform[0,1].
is Uniform[0,1].
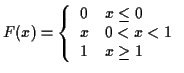

Example: ![]() is exponential.
is exponential.