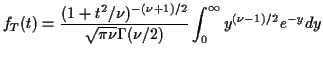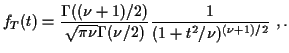Theorem:
Suppose
![]() are independent
are independent
![]() random
variables.
Then
random
variables.
Then
Proof: Let
![]() .
.
Then
![]() are
independent
are
independent ![]() .
.
So
![]() is multivariate
standard normal.
is multivariate
standard normal.
Note that
![]() and
and
![]() Thus
Thus
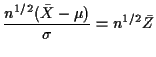
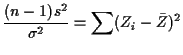
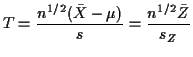
So: reduced to ![]() and
and ![]() .
.
Step 1: Define
![$\displaystyle Y =\left[\begin{array}{cccc}
\frac{1}{\sqrt{n}} &
\frac{1}{\sqrt{...
...]
\left[\begin{array}{c}
Z_1 \\
Z_2 \\
\vdots
\\
Z_n
\end{array}\right]
$](img23.gif)
![$\displaystyle = \left[\begin{array}{c\vert cccc} 1 & 0 & 0 & \cdots & 0 \\ \hli...
...ots & -\frac{1}{n} \\ 0 & \vdots & \cdots & & 1-\frac{1}{n} \end{array} \right]$](img29.gif) |
||
![$\displaystyle = \left[\begin{array}{c\vert c} 1 & 0 \\ \hline \\ 0 & Q \end{array} \right] \, .$](img30.gif) |
Solve for ![]() from
from ![]() :
:
![]() for
for
![]() . Use the identity
. Use the identity
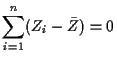
![$\displaystyle \Sigma^{-1} \equiv (MM^t)^{-1} =
\left[\begin{array}{c\vert c}
1 & 0
\\
\hline
\\
0 & Q^{-1}
\end{array}\right]
$](img35.gif)
Use change of variables to find ![]() .
Let
.
Let
![]() denote vector whose
entries are
denote vector whose
entries are
![]() . Note that
. Note that
![$\displaystyle \frac{(2\pi)^{-(n-1)/2}\exp[-{\bf y}_2^t Q^{-1} {\bf y}_2/2]}{\vert\det M\vert}$](img44.gif) |
Note: ![]() is ftn of
is ftn of ![]() times a
ftn of
times a
ftn of
![]() .
.
Thus
![]() is independent of
is independent of
![]() .
.
Since ![]() is a function of
is a function of
![]() we see that
we see that
![]() and
and
![]() are independent.
are independent.
Also, density of ![]() is a multiple of the function of
is a multiple of the function of ![]() in
the factorization above. But factor is standard normal
density so
in
the factorization above. But factor is standard normal
density so
![]() .
.
First 2 parts done. Third part is a homework exercise.
Derivation of the ![]() density:
density:
Suppose
![]() are independent
are independent ![]() . Define
. Define
![]() distribution to be that of
distribution to be that of
![]() .
Define angles
.
Define angles
![]() by
by
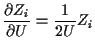
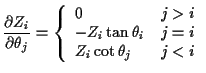
Fix ![]() to clarify the formulas.
to clarify the formulas.
Use shorthand
![]() .
.
Matrix of partial derivatives is
![$\displaystyle \left[\begin{array}{ccc}
\frac{\cos\theta_1}{2R}
&
-R \sin\theta_...
...R}
&
R cos\theta_1\sin\theta_2
&
R \sin\theta_1\cos\theta_2
\end{array}\right]
$](img75.gif)
Resulting matrix is lower triangular; diagonal entries
![]() ,
,
![]() and
and
![]() .
.
We multiply these together to get
General ![]() : every term in the first column contains a factor
: every term in the first column contains a factor
![]() while
every other entry has a factor
while
every other entry has a factor ![]() .
.
FACT: Multiplying a column in a matrix by ![]() multiplies
the determinant by
multiplies
the determinant by ![]() .
.
SO: Jacobian of the transformation is
![]() times
some function, say
times
some function, say ![]() , which depends only on the angles.
, which depends only on the angles.
Thus the joint density
of
![]() is
is
Answer has the form
Evaluate ![]() by making
by making
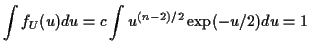
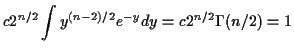
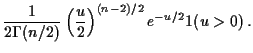
Fourth part: consequence of
first 3 parts and def'n of ![]() distribution.
distribution.
Defn:
![]() if
if ![]() has same distribution
as
has same distribution
as
Derive density of ![]() in this definition:
in this definition:
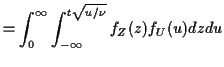 |
![$\displaystyle \frac{d}{dt} P(T \le t) =
\int_0^\infty f_U(u)
\left(\frac{u}{\nu}\right)^{1/2}
\frac{\exp[-t^2u/(2\nu)]}{\sqrt{2\pi}} du
$](img110.gif)
Plug in
![$\displaystyle f_T(t) = \frac{\int_0^\infty (u/2)^{(\nu-1)/2}
\exp[-u(1+t^2/\nu)/2]du
}{2\sqrt{\pi\nu}\Gamma(\nu/2)} \, .
$](img112.gif)