Definition:
![]() iff
iff

Definition:
![]() iff
iff
![]() (a column vector for later use) with the
(a column vector for later use) with the
![]() independent and each
independent and each
![]() .
.
In this case,
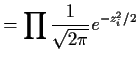 |
||
Definition: ![]() has a multivariate normal distribution if it
has the same distribution as
has a multivariate normal distribution if it
has the same distribution as ![]() for some
for some
![]() , some
, some
![]() matrix of constants
matrix of constants ![]() and
and
![]() .
.
Lemma: The matrix ![]() can be taken to be square with
no loss of generality.
can be taken to be square with
no loss of generality.
Proof: The simplest proof involves multivariate characteristic functions:
If the matrix ![]() is singular then
is singular then ![]() will not have a density. If
will not have a density. If ![]() is
invertible then we can derive the multivariate normal density
by the change of variables formula:
is
invertible then we can derive the multivariate normal density
by the change of variables formula:
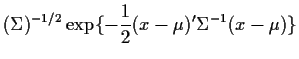
Properties of the ![]() distribution
distribution
![$\displaystyle X = \left[\begin{array}{c} X_1\\ X_2\end{array} \right]
$](img38.gif)
![$\displaystyle \mu = \left[\begin{array}{c} \mu_1\\ \mu_2\end{array} \right]
$](img39.gif)
![$\displaystyle \Sigma = \left[\begin{array}{cc} \Sigma_{11} & \Sigma_{12}
\\
\Sigma_{21} & \Sigma_{22} \end{array} \right]
$](img40.gif)
If ![]() is an
is an ![]() process then
process then
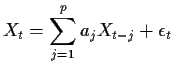
![$\displaystyle \left[\begin{array}{cc}C(0) & C(q) \\ C(q) & C(0) \end{array}\right]
$](img63.gif)
![$\displaystyle \left[\begin{array}{ccc}
C(1) & \cdots & C(p)
\\
C(q-1)& \cdots & C(q-p)
\end{array}\right]
$](img69.gif)
To use this idea we define the partial autocorrelation function to be
Qualitative idea: A plot of the sample partial
autocorrelation function (derived by replacing ![]() by
by ![]() in the definition of
in the definition of ![]() ) is examined. For an
) is examined. For an ![]() process
this sample plot ought to drop suddenly to 0 for
process
this sample plot ought to drop suddenly to 0 for ![]() .
.
Now I calculate ![]() for a mean 0
for a mean 0 ![]() process. We have
process. We have
![]() . Let
. Let
![$\displaystyle \left[\begin{array}{c}Y \\ Z\end{array}\right]
=
\left[\begin{array}{c} X_t \\ X_{t-2} \\ X_{t-1}\end{array}\right]
$](img83.gif)
![$\displaystyle \Sigma = C_X(0)\left[\begin{array}{ccc}
1 & \rho^2 & \rho
\\
\rho^2 & 1 & \rho
\\
\rho & \rho & 1
\end{array}\right]
$](img88.gif)
![$\displaystyle \Sigma_{11} = \Sigma = C_X(0)\left[\begin{array}{cc}
1 & \rho^2 \\ \rho^2 & 1\end{array}\right]
$](img91.gif)
![$\displaystyle \Sigma_{12} = C_X(0)\left[\begin{array}{c}\rho\\ \rho \end{array} \right]
$](img92.gif)
| Cov |
||
![$\displaystyle = C_X(0)\left[\begin{array}{cc} 1 & \rho^2 \\ \rho^2 & 1\end{arra...
...)\left[\begin{array}{cc} \rho^2 & \rho^2 \\ \rho^2 & \rho^2 \end{array} \right]$](img96.gif) |
||
![$\displaystyle = C_X(0) \left[\begin{array}{cc} 1-\rho^2 & 0 \\ 0 & 1-\rho^2 \end{array} \right]$](img97.gif) |
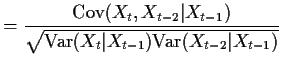 |
||
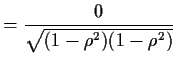 |
||
Consider the problem of prediction ![]() knowing
knowing
![]() .
In this course we choose a predictor
.
In this course we choose a predictor
![]() to minimize the mean squared prediction error:
to minimize the mean squared prediction error:
![$\displaystyle (X_t\vert X_{t-1},\ldots,X_{t-K}) = \mu+A\left[\begin{array}{c}
X_{t-1} - \mu \\ \vdots \\ X_{t-k}-\mu \end{array}\right]
$](img107.gif)
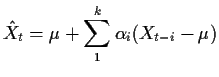
| E |
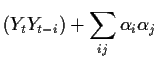 E E |
|
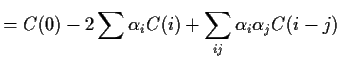 |

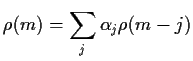
Remark: This makes it look as if you would compute the
first 40 values of the PACF by solving 40 different problems and picking out the
last ![]() in each one but in fact there is an explicit recursive
algorithm to compute these things.
in each one but in fact there is an explicit recursive
algorithm to compute these things.
To estimate the PACF you can either estimate the ACF and do the arithmetic above with estimates instead of theoretical values or minimize a sample version of the mean squared prediction error:
The Mean Squared Prediction Error is
![$\displaystyle \left\{[ (X_t - \mu - \sum_{j-1}^k \alpha_k (X_{t-k} - \mu)]^2\right\}
$](img126.gif)
![$\displaystyle \sum_{t=k}^{T-1}\left \{[ (X_t -\bar{X}-\sum_{j-1}^k \alpha_k (X_{t-k} - \mu)]^2\right\}/T
$](img128.gif)
![$\displaystyle Y = \left[\begin{array}{c} X_k-\bar{X} \\ \vdots \\ X_{T-1} - \bar{X}
\end{array}\right]
$](img129.gif)
![$\displaystyle Z = \left[\begin{array}{ccc}
X_{t-1} - \bar{X} & \cdots & X_0 - \...
...vdots
\\
X_{T-2} - \bar{X} & \cdots & X_{T-k-1} - \bar{X}
\end{array}\right]
$](img130.gif)
What follows are plots of 5 series, their fitted ACFs and their fitted PACFs. The series are:
Here is the SPlus code I used to make the following plots. You should note the use of the function acf which calculates and plots ACF and PACF.
#
# Comments begin with #
#
# Begin by generating the series. The AR series generated are NOT
# stationary. But I generate 10000 values from the recurrence relation
# and use the last 500. Asymptotic stationarity should guarantee that
# these last 500 are pretty stationary.
#
n<- 10000
ep <- rnorm(n)
ma2 <- ep[3:502]+0.8*ep[2:501]-0.9*ep[1:500]
ar2 <- rep(0,n)
ar2[1:2] <- ep[1:2]
for(i in 3:n) {ar2[i] <- ep[i]
+ ar2[i-1] -0.99*ar2[i-2]}
ar2 <- ar2[(n-499):n]
ar2 <- ts(ar2)
ar3 <- rep(0,n)
ar3[1:3] <- ep[1:3]
for(i in 4:n) {ar3[i] <- ep[i] + 0.8*ar3[i-1]
-ar3[i-2]/3 +(0.8/1.712)*ar3[i-3]}
ar3 <- ar3[(n-499):n]
ar3 <- ts(ar3)
#
# The next line turns on a graphics device -- in this case the
# graph will be made in postscript in a file called ma2.ps. It
# will come out in portrait, not landscape, format.
#
postscript(file="ma2.ps",horizontal=F)
#
# The next line says to put 3 pictures
# in a single column on the plot
#
par(mfcol=c(3,1))
tsplot(ma2,main="MA(2) series")
acf(ma2)
acf(ma2,type="partial")
#
# When you finish a picture you turn
# off the graphics device
# with the next line.
#
dev.off()
#
#
#
postscript(file="ar2.ps",horizontal=F)
par(mfcol=c(3,1))
tsplot(ar2,main="AR(2) series")
acf(ar2)
acf(ar2,type="partial")
dev.off()
#
#
postscript(file="ar3.ps",horizontal=F)
par(mfcol=c(3,1))
tsplot(ar3,main="AR(3) series")
acf(ar3)
acf(ar3,type="partial")
dev.off()
#
#
postscript(file="sunspots.ps",horizontal=F)
par(mfcol=c(3,1))
tsplot(sunspots,main="Sunspots series")
acf(sunspots,lag.max=480)
acf(sunspots,lag.max=480,type="partial")
dev.off()
#
#
postscript(file="rain.nyc1.ps",horizontal=F)
par(mfcol=c(3,1))
tsplot(rain.nyc1,main="New York Rain Series")
acf(rain.nyc1)
acf(rain.nyc1,type="partial")
dev.off()





You should notice: