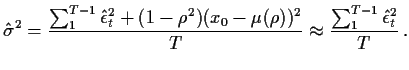STAT 804: Notes on Lecture 7

Model identification summary: The simplest model identification tactic is to look for either a pure MA or pure AR model. To do so:

1. Compute the sample autocorrelation function. Plot $\widehat{ACF}(h)$ against $h$. If the process is an $MA(q)$ then the ACF will be 0 after lag $q$.

2. Compute the sample partial autocorrelation function. Plot the estimated $PACF(h)$ against $h$. If the process is an $AR(p)$ then the PACF will be 0 after lag $p$.

Non stationary processes

If $X$ is not stationary we will need to transform $X$ to find a related stationary series. We will consider in this course two sorts of non-stationarity -- non constant mean and integration.

Non constant mean: If E$(X_t)$ is not constant we will hope to model $\mu_t=$E$(X_t)$ using a small number of parameters and then model $Y_t = X_t-\mu_t$ as a stationary series. Three common structures for $\mu_t$ are linear, polynomial and periodic:

Linear trend: Suppose

$$\mu_t = \alpha+\beta t$$

We seek to estimate $\alpha$ and $\beta$ in order to analyze $Y_t = X_t - \alpha-\beta t$.

Method 1: regression (detrending). We regress $X_t$ on $t$ to get $\hat\alpha$ and $\hat\beta$ and analyze

$$\hat{Y}_t =X_t-\hat\alpha-\hat\beta t$$

We hope

$$\hat{Y} \approx Y$$

Method 2: differencing. Define

$$W_t = X_t-X_{t-1}$$

$$= \left[(I-B)X\right]_t$$

Then

$$W_t = \left[(\alpha+\beta t +Y_t) - (\alpha+\beta (t-1) +Y_{t-1})\right]$$

$$= \beta+Y_{t}-Y_{t-1}$$

Since this is a linear filter applied to the series $Y$ it is stationary if $Y$ is. BUT, it might be stationary even if $Y$ is not. Suppose that $\epsilon_t$ is an iid mean 0 sequence. Then

$$Y_t = \sum_1^t \epsilon_j$$

is a random walk. Notice that $Y_t-Y_{t-1}=\epsilon_t$ is stationary. To see that $Y_t$, the random walk, is not stationary notice that Var$(Y_t) = t$Var$(\epsilon_1)$.

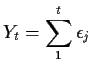
These random walk models are common in Economics. In physics they are used in the limit of very small time increments - this leads to Brownian motion.

Definition: $X$ satisfies an ARIMA$(p,d,q)$ model if

$$\phi(B) \nabla^d X = \psi(B) \epsilon$$

where

1. $\epsilon$ is white noise,

2. $\phi$ is a polynomial of degree $p$,

3. $\psi$ is a polynomial of degree $q$,

4. $\nabla = I-B$ is the differencing operator.

Remark: If $X_t = \mu_t+Y_t$ where $Y$ is stationary and $\mu$ is a polynomial of degree less than or equal to $p$ then $\nabla^d X$ is stationary. (So a cubic shaped trend could be removed by differencing 3 times.)

WARNING: it is a common mistake in students' data analyses to over difference. When you difference a stationary $ARMA(p,q)$ you introduce a unit root in the defining polynomial - the result cannot be written as an infinite order moving average.

Detrending: Define a response vector

$$U = \left[\begin{array}{c} X_0 \\ \vdots \\ X_{T-1} \end{array} \right]$$

and a design matrix by

$$V=\left[\begin{array}{cc} 1 & 0 \\ 1 & 1 \\ \vdots & \vdots \\ 1 & T-1 \end{array}\right]$$

and write

$$U = V\theta +Y$$

with

$$Y = \left[\begin{array}{c} Y_0 \\ \cdots \\ Y_{T-1} \end{array} \right]$$

and

$$\theta = \left[\begin{array}{c} \alpha \\ \beta\end{array}\right] \, .$$

Then we estimate by

$$\hat\theta = (V^TV)^{-1} V^T U$$

Our detrended series is

$$\hat{Y} = U-V\hat\theta$$

$$= (I-V(V^TV)^{-1} V^T)U$$

Now since Cov$(Y) \neq \sigma^2 I$ ordinary least squares is not strictly appropriate. In general in the model

$$U=V\theta+W$$

where $W$ has mean 0 and variance covariance matrix $\Sigma$, the minimum variance linear estimator of $\theta$ is the generalized least squares estimate

$$\hat\theta_{GLS} = (V^T \Sigma^{-1} V)^T V^T \Sigma^{-1} U \, .$$

This estimate is unbiased and has variance

$$(V^T \Sigma^{-1} V)^{-1}$$

For this model the ordinary least squares estimate is also unbiased and has variance

$$(V^TV)^{-1} V^T \Sigma V (V^TV)^{-1}$$

The problem in our context (it is almost always a problem) is that you can only use $\hat\theta_{GLS}$ if you know $\Sigma$. In our context you won't know $\Sigma$ until you have removed a trend, selected a suitable $ARMA$ model and estimated the parameters. The natural proposal is to follow an iterative process:

1. Fit the linear model by ordinary least squares.

2. Compute the residual series.

3. Identify a suitable $ARMA(p,q)$ model.

4. Fit the parameters of this model.

5. Using the estimates compute an estimated variance covariance of the residual process.

6. Refit the linear model in step 1 using Generalized Least Squares with the variance covariance as estimated in the previous step, then go back to 2).

The process is repeated until the estimates stop changing in any important way.

Folklore: There is evidence that the OLS estimator has a variance which is not too much different from GLS in common ARMA models.

Seasonal Non-stationarity

Every winter the measured (not reported) unemployment rate in Canada rises. A simple model which has this feature has a non-stationary mean of the form

$$\mu_{t+S}=\mu_t$$

Typically the value of $S$ is 12 for monthly data or 4 for quarterly data (common in economic data). Normally, $\mu_1,\ldots,\mu_S$ are not the same, of course.

Definition: Deseasonalization is the process of transforming $X$ to eliminate this sort of seasonal variation in the mean.

Method 1: Regression. Estimate

$$\hat\mu_t = \frac{X_t+X_{t+S} + \cdots }{\char93 \text{ of terms}}$$

and then

$$\hat{Y}_t = X_t - \hat\mu_t$$

This is ordinary least squares regression with

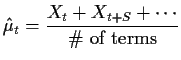
$$\theta = \left[\begin{array}{c} \mu_0 \\ \vdots \\ \mu_{S-1} \end{array}\right]$$

and

$$V=\left[\begin{array}{ccccc} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & ... ...\ \vdots & \vdots & \vdots & \vdots & \vdots \end{array}\right]_{T \times S}$$

Method B: Seasonal differencing:

$$W_t = X_{t+S} - X_t$$

is stationary. BUT: if $Y$ was an ARMA process then now $W$ has a unit root.

Definition: A multiplicative $ARIMA(p,d,q) \times (P,D,Q)_S$ model has the form:

$$\Phi(B^S) \phi(B) (I-B^S)^D (I-B)^d X = \Psi(B^S) \psi(B) \epsilon$$

where $\Phi,\phi,\Psi,\psi$ are polynomials of degree $P,p,Q,q$ respectively with all roots outside the unit circle (and other technical conditions - see assignment 2, question 1) and $\epsilon$ is white noise.

As an example consider the model

$$(1-\Phi_1 B^{12})(1-\phi_1B)X = (1-\Psi_1 B^{12} )(1-\psi_1B) \epsilon$$

which is an $ARIMA(1,0,1) \times (1,0,1)_{12}$ model. Multiplying this out we get

$$(I -\phi_1 B -\Phi_1B^{12} + \phi_1\Phi_1 B^{13}) X = (I -\psi_1 B -\Psi_1B^{12} + \psi_1\Psi_1 B^{13}) \epsilon$$

which looks like an $ARMA(13,13)$. The key point is that this new model has only 4 parameters (plus the variance of $\epsilon$) instead of the 26 for a general $ARMA(13,13)$.

Fitting $ARIMA(p,d,q)$ models to data

Fitting the $I$ part is easy we simply difference $d$ times. The same observation applies to seasonal multiplicative model. Thus to fit an ARIMA$(p,d,q)$ model to $X$ you compute $Y =(I-B)^d X$ (shortening your data set by $d$ observations) and then you fit an $ARMA(p,q)$ model to $Y$. So we assume that $d=0$.

Simplest case: fitting the AR(1) model

$$X_t = \mu+\rho(X_{t-1}-\mu) + \epsilon_t$$

We must estimate 3 parameters: $\mu, \rho$ and $\sigma^2=$Var$(\epsilon_t)$.

Our basic strategy will be:

• Estimate the parameters by maximum likelihood as if the series were Gaussian.

• Investigate the properties of the estimates for non-Gaussian data.

Generally the full likelihood is rather complicated; we will use conditional likelihoods and ad hoc estimates of some parameters to simplify the situation.

The likelihood: Gaussian data

If the errors $\epsilon$ are normal then so is the series $X$. In general the vector $X=(X_0,\ldots,X_{T-1})^t$ has a $MVN({\bf\mu},\Sigma)$ where $\Sigma_{ij} = C(i-j)$ and ${\bf\mu}$ is a vector all of whose entries are $\mu$. The joint density of $X$ is

$$f_X(x) = \frac{1}{(2\pi)^{T/2} \det(\Sigma)^{1/2}} \exp\left\{-\frac{1}{2} (x-{\bf\mu})^t \Sigma^{-1} (x-{\bf\mu})\right\}$$

so that the log likelihood is

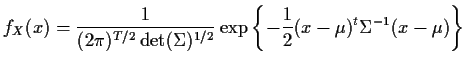
$$\ell(\mu,a_1,\ldots,a_p,b_1,\ldots,b_q,\sigma) = -\frac{1}{2}\left[ (x-{\bf\mu})^t \Sigma^{-1} (x-{\bf\mu}) + \log(\det(\Sigma))\right]$$

Here I have indicated precisely (for an $ARMA(p,q)$) the parameters on which the quantity depends.

It is possible to carry out full maximum likelihood by maximizing the quantity in question numerically. In general this is hard, however.

Here I indicate some standard tactics. In your homework I will be asking you to carry through this analysis for one particular model.

The $AR(1)$ model

Consider the model

$$X_t-\mu = \rho(X_{t-1} - \mu) + \epsilon_t$$

This model formula permits us to write down the joint density of $X$ in a simpler way:

$$f_X = f_{X_{T-1}\vert X_{T-2},\ldots,X_0} f_{X_{T-2}\vert X_{T-3},\ldots,X_0}\cdots f_{X_1\vert X_0} f_{X_0}$$

Each of the conditional densities is simply

$$f_{X_{k+1}\vert X_k,\ldots,X_0} (x_k\vert x_{k-1},\ldots,x_{0}) = g\left[x_k-\mu-\rho(x_{k-1}-\mu)\right]$$

where $g$ is the density of an individual $\epsilon$. For iid $N(0,\sigma^2)$ errors this gives a log likelihood which is

$$\ell(\mu,\rho,\sigma) = - \frac{1}{2\sigma^2}\sum_1^{T-1} \left[x_k-\mu-\rho(x_{k-1}-\mu)\right]^2 -(T-1)\log(\sigma) + \log(f_{X_0})$$

Now for a stationary series I showed that $X_t \sim N(\mu,\sigma^2/(1-\rho^2))$ so that

$$\log(f_{X_0}(x_0)) = -\frac{1-\rho^2}{2\sigma^2}(x_0-\mu)^2 -\log(\sigma) + \log(1-\rho^2)$$

This makes

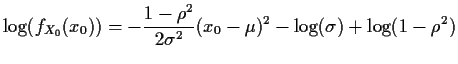
$$\ell(\mu,\rho,\sigma) = - \frac{1}{2\sigma^2} \left\{ \sum_1^{T-1}\left[x_k-\mu-\rho(x_{k-1}-\mu)\right]^2 +(1-\rho^2)(x_0-\mu)^2\right\}$$

$$\qquad -T\log(\sigma) + \log(1-\rho^2)$$

We can maximize this over $\mu$ and $\sigma$ explicitly. First

$$\frac{\partial}{\partial\mu} \ell = \frac{1}{\sigma^2} \left\{ \s... ...}\left[x_k-\mu-\rho(x_{k-1}-\mu)\right](1-\rho) + (1-\rho^2)(x_0-\mu)\right\}$$

Set this equal to 0 to find

$$\hat\mu(\rho) = \frac{ (1-\rho)\sum_1^{T-1}(x_k -\rho x_{k-1}) + (1-\rho^2)x_0}{1-\rho^2 +(1-\rho)^2(T-1)}$$

$$= \frac{ \sum_1^{T-1}(x_k -\rho x_{k-1}) +(1+\rho)x_0}{1+\rho+ (1-\rho)(T-1)}$$

Notice that this estimate is free of $\sigma$ and that if $T$ is large we may drop the 1 in the denominator and the term involving $x_0$ in the denominator and get

$$\hat\mu(\rho) \approx \frac{\sum_1^{T-1}(x_k -\rho x_{k-1})}{(T-1)(1-\rho)}$$

Finally, the numerator is actually

$$\sum_0^{T-1} x_k - x_0 -\rho(\sum_0^{T-1} x_k -x_{T-1}) = (1-\rho) \sum_0^{T-1} x_k -x_0 +\rho x_{T-1}$$

The last two terms here are smaller than the sum; if we neglect them we get

$$\hat\mu(\rho) \approx \bar{X} \, .$$

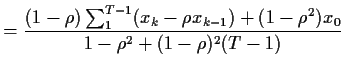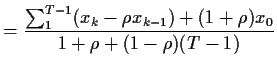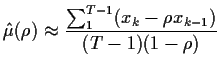
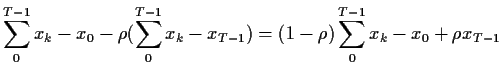
Now compute

$$\frac{\partial}{\partial\sigma} \ell = \frac{1}{\sigma^3}\left\{ ... ...mu-\rho(x_{k-1}-\mu)\right]^2 +(1-\rho^2)(x_0-\mu)^2\right\} -\frac{T}{\sigma}$$

and set this to 0 to find

$$\hat\sigma^2(\rho) = \frac{\left\{ \sum_1^{T-1}\left[x_k-\mu(\rho)-\rho(x_{k-1}-\mu(\rho))\right]^2 +(1-\rho^2)(x_0-\mu(\rho))^2\right\}}{T}$$

When $\rho$ is known it is easy to check that $(\mu(\rho),\sigma(\rho))$ maximizes $\ell(\mu,\rho,\sigma)$.

To find $\hat\rho$ you now plug $\hat\mu(\rho)$ and $\hat\sigma(\rho)$ into $\ell$ (getting the so called profile likelihood $\ell(\hat\mu(\rho),\rho,\hat\sigma(\rho))$) and maximize over $\rho$. Having thus found $\hat\rho$ the mles of $\mu$ and $\hat\sigma$ are simply $\hat\mu(\hat\rho)$ and $\hat\sigma(\hat\rho)$.

It is worth observing that fitted residuals can then be calculated:

$$\hat\epsilon_t = (X_t-\hat\mu) - \hat\rho(X_{t-1}-\hat\mu)$$

(There are only $T-1$ of them since you cannot easily estimate $\epsilon_0$.) Note, too, that the formula for $\hat\sigma^2$ simplifies to

$$\hat\sigma^2 = \frac{ \sum_1^{T-1} \hat\epsilon_t^2 +(1-\rho^2)(x_0-\mu(\rho))^2}{T} \approx \frac{ \sum_1^{T-1} \hat\epsilon_t^2 }{T} \, .$$