NLOPTIONS Statement

The CALIS Procedure

NLOPTIONS Statement

NLOPTIONS option(s) ;

Many options that are available in PROC NLP can now be specified for the optimization subroutines in PROC CALIS using the NLOPTIONS statement. The NLOPTIONS statement provides more displayed and file output on the results of the optimization process, and it permits the same set of termination criteria as in PROC NLP. These are more technical options that you may not need to specify in most cases. The available options are summarized in Table 19.2 through Table 19.4, and the options are described in detail in the following three sections.

Table 19.2: Options Documented in the PROC CALIS Statement


Option	Short Description
Estimation Methods
G4=i	algorithm for computing STDERR

Optimization Techniques
TECHNIQUE=name	minimization method
UPDATE=name	update technique
LINESEARCH=i	line-search method
FCONV=r	relative change function convergence criterion
GCONV=r	relative gradient convergence criterion
INSTEP=r	initial step length (SALPHA=, RADIUS=)
LSPRECISION=r	line-search precision
MAXFUNC=i	maximum number of function calls
MAXITER=i <n>	maximum number of iterations

Miscellaneous Options
ASINGULAR=r	absolute singularity criterion for inversion of the information matrix
COVSING=r	singularity tolerance of the information matrix
MSINGULAR=r	relative M singularity criterion for inversion of the information matrix
SINGULAR=r	singularity criterion for inversion of the Hessian
VSINGULAR=r	relative V singularity criterion for inversion of the information matrix

Table 19.3: Termination Criteria Options


Option	Short Description
Options Used by All Techniques
ABSCONV=r	absolute function convergence criterion
MAXFUNC=i	maximum number of function calls
MAXITER=i <n>	maximum number of iterations
MAXTIME=r	maximum CPU time
MINITER=i	minimum number of iterations

Options for Unconstrained and Linearly Constrained Techniques
ABSFCONV=r <n>	absolute change function convergence criterion
ABSGCONV=r <n>	absolute gradient convergence criterion
ABSXCONV=r <n>	absolute change parameter convergence criterion
FCONV=r <n>	relative change function convergence criterion
FCONV2=r <n>	function convergence criterion
FDIGITS=r	precision in computation of the objective function
FSIZE=r	parameter for FCONV= and GCONV=
GCONV=r <n>	relative gradient convergence criterion
GCONV2=r <n>	relative gradient convergence criterion
XCONV=r <n>	relative change parameter convergence criterion
XSIZE=r	parameter for XCONV=

Options for Nonlinearly Constrained Techniques
ABSGCONV=r <n>	maximum absolute gradient of Lagrange function criterion
FCONV2=r <n>	predicted objective function reduction criterion
GCONV=r <n>	normalized predicted objective function reduction criterion

Table 19.4: Miscellaneous Options


Option	Short Description
Options for the Approximate Covariance Matrix of Parameter Estimates
CFACTOR=r	scalar factor for STDERR
NOHLF	use Hessian of the objective function for STDERR

Options for Additional Displayed Output
PALL	display initial and final optimization values
PCRPJAC	display approximate Hessian matrix
PHESSIAN	display Hessian matrix
PHISTORY	display optimization history
PINIT	display initial values and derivatives (PALL)
PNLCJAC	display Jacobian matrix of nonlinear constraints (PALL)
PRINT	display results of the optimization process

Additional Options for Optimization Techniques
DAMPSTEP< =r >	controls initial line-search step size
HESCAL=n	scaling version of Hessian or Jacobian
LCDEACT=r	Lagrange multiplier threshold of constraint
LCEPSILON=r	range for boundary and linear constraints
LCSINGULAR=r	QR decomposition linear dependence criterion
NOEIGNUM	suppress computation of matrices
RESTART=i	restart algorithm with a steepest descent direction
VERSION=1 \| 2	quasi-Newton optimization technique version

Options Documented in the PROC CALIS Statement

The following options are the same as in the PROC CALIS statement and are documented in the section "PROC CALIS Statement".

Estimation Method Option

G4=i: specifies the method for computing the generalized (G2 or G4) inverse of a singular matrix needed for the approximate covariance matrix of parameter estimates. This option is valid only for applications where the approximate covariance matrix of parameter estimates is found to be singular.

Optimization Technique Options

TECHNIQUE | TECH=name
OMETHOD | OM=name: specifies the optimization technique.
UPDATE | UPD=name: specifies the update method for the quasi-Newton or conjugate-gradient optimization technique.
LINESEARCH | LIS=i: specifies the line-search method for the CONGRA, QUANEW, and NEWRAP optimization techniques.
FCONV | FTOL=r: specifies the relative function convergence criterion. For more details, see the section "Termination Criteria Options".
GCONV | GTOL=r: specifies the relative gradient convergence criterion. For more details, see the section "Termination Criteria Options".
INSTEP | SALPHA | RADIUS=r: restricts the step length of an optimization algorithm during the first iterations.
LSPRECISION | LSP=r: specifies the degree of accuracy that should be obtained by the line-search algorithms LIS=2 and LIS=3.
MAXFUNC | MAXFU=i: specifies the maximum number i of function calls in the optimization process. For more details, see the section "Termination Criteria Options".
MAXITER | MAXIT=i <n>: specifies the maximum number i of iterations in the optimization process. For more details, see the section "Termination Criteria Options".

Miscellaneous Options

ASINGULAR | ASING=r: specifies an absolute singularity criterion r, r > 0, for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates.
COVSING=r: specifies a nonnegative threshold r, r > 0, that decides whether the eigenvalues of the information matrix are considered to be zero. This option is valid only for applications where the approximate covariance matrix of parameter estimates is found to be singular.
MSINGULAR | MSING=r: specifies a relative singularity criterion r, r > 0, for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates.
SINGULAR | SING =r: specifies the singularity criterion r, $0 \leq r \leq 1$ , that is used for the inversion of the Hessian matrix. The default value is 1E-8.
VSINGULAR | VSING=r: specifies a relative singularity criterion r, r > 0, for the inversion of the information matrix, which is needed to compute the approximate covariance matrix of parameter estimates.

Termination Criteria Options

Let x^* be the point at which the objective function f(·) is optimized, and let x^(k) be the parameter values attained at the kth iteration. All optimization techniques stop at the kth iteration if at least one of a set of termination criteria is satisfied. The specified termination criteria should allow termination in an area of sufficient size around x^*. You can avoid termination respective to any of the following function, gradient, or parameter criteria by setting the corresponding option to zero. There is a default set of termination criteria for each optimization technique; most of these default settings make the criteria ineffective for termination. PROC CALIS may have problems due to rounding errors (especially in derivative evaluations) that prevent an optimizer from satisfying strong termination criteria.

Note that PROC CALIS also terminates if the point x^(k) is fully constrained by linearly independent active linear or boundary constraints, and all Lagrange multiplier estimates of active inequality constraints are greater than a small negative tolerance.

The following options are available only in the NLOPTIONS statement (except for FCONV, GCONV, MAXFUNC, and MAXITER), and they affect the termination criteria.

Options Used by All Techniques

The following five criteria are used by all optimization techniques.

ABSCONV | ABSTOL=r

specifies an absolute function convergence criterion.

For minimization, termination requires

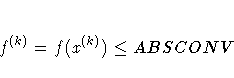
$f^{(k)} = f(x^{(k)}) \leq ABSCONV$
For maximization, termination requires

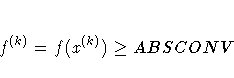
$f^{(k)} = f(x^{(k)}) \geq ABSCONV$

The default value of ABSCONV is

for minimization, the negative square root of the largest double precision value
for maximization, the positive square root of the largest double precision value

MAXFUNC | MAXFU=i

requires the number of function calls to be no larger than i. The default values are listed in the following table.

TECH=	MAXFUNC default
LEVMAR, NEWRAP, NRRIDG, TRUREG	i=125
DBLDOG, QUANEW	i=500
CONGRA	i=1000

The default is used if you specify MAXFUNC=0. The optimization can be terminated only after completing a full iteration. Therefore, the number of function calls that is actually performed can exceed the number that is specified by the MAXFUNC= option.

MAXITER | MAXIT= i <n>

requires the number of iterations to be no larger than i. The default values are listed in the following table.

TECH=	MAXITER default
LEVMAR, NEWRAP, NRRIDG, TRUREG	i=50
DBLDOG, QUANEW	i=200
CONGRA	i=400

The default is used if you specify MAXITER=0 or missing.

The optional second value n is valid only for TECH=QUANEW with nonlinear constraints. It specifies an upper bound n for the number of iterations of an algorithm and reduces the violation of nonlinear constraints at a starting point. The default value is n=20. For example, specifying MAXITER= . 0 means that you do not want to exceed the default number of iterations during the main optimization process and that you want to suppress the feasible point algorithm for nonlinear constraints.

MAXTIME=r

requires the CPU time to be no larger than r. The default value of the MAXTIME= option is the largest double floating point number on your computer.

MINITER | MINIT=i

specifies the minimum number of iterations. The default value is i=0.

The ABSCONV=, MAXITER=, MAXFUNC=, and MAXTIME= options are useful for dividing a time-consuming optimization problem into a series of smaller problems by using the OUTEST= and INEST= data sets.

Options for Unconstrained and Linearly Constrained Techniques

This section contains additional termination criteria for all unconstrained, boundary, or linearly constrained optimization techniques.

ABSFCONV | ABSFTOL=r <n>

specifies the absolute function convergence criterion. Termination requires a small change of the function value in successive iterations,

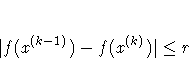
$| f(x^{(k-1)}) - f(x^{(k)})| \leq r$

The default value is r=0. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

ABSGCONV | ABSGTOL=r <n>

specifies the absolute gradient convergence criterion. Termination requires the maximum absolute gradient element to be small,

$\max_j | g_j^{(k)}| \leq r$

The default value is r=1E-5. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

Note:: In some applications, the small default value of the ABSGCONV= criterion is too difficult to satisfy for some of the optimization techniques.

ABSXCONV | ABSXTOL=r <n>

specifies the absolute parameter convergence criterion. Termination requires a small Euclidean distance between successive parameter vectors,

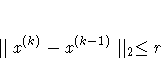
$\parallel x^{(k)} - x^{(k-1)} \parallel_2 \leq r$

The default value is r=0. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

FCONV | FTOL=r <n>

specifies the relative function convergence criterion. Termination requires a small relative change of the function value in successive iterations,

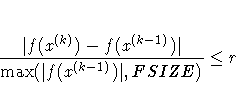
${ | f(x^{(k)}) - f(x^{(k-1)})| \over \max(| f(x^{(k-1)})|,FSIZE) } \leq r$

where FSIZE is defined by the FSIZE= option. The default value is r=10^-FDIGITS, where FDIGITS either is specified or is set by default to $-\log_{10}(\epsilon)$ , where $\epsilon$ is the machine precision. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

FCONV2 | FTOL2=r <n>

specifies another function convergence criterion. For least-squares problems, termination requires a small predicted reduction

$df^{(k)} \approx f(x^{(k)}) - f(x^{(k)} + s^{(k)})$

of the objective function.

The predicted reduction

$df^{(k)} & = & -g^{(k)^'} s^{(k)} - {1 \over 2} s^{(k)^'} G^{(k)} s^{(k)} \ & = & -{1 \over 2} s^{(k)^'} g^{(k)} \ & \leq & r$

is computed by approximating the objective function f by the first two terms of the Taylor series and substituting the Newton step

s^(k) = - G^(k)-1 g^(k)

The FCONV2 criterion is the unscaled version of the GCONV criterion. The default value is r=0. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

FDIGITS=r

specifies the number of accurate digits in evaluations of the objective function. Fractional values such as FDIGITS=4.7 are allowed. The default value is $r=-log_{10}\epsilon$ , where $\epsilon$ is the machine precision. The value of r is used for the specification of the default value of the FCONV= option.

FSIZE=r

specifies the FSIZE parameter of the relative function and relative gradient termination criteria. The default value is r=0. See the FCONV= and GCONV= options.

GCONV | GTOL=r <n>

specifies the relative gradient convergence criterion. For all techniques except the CONGRA technique, termination requires that the normalized predicted function reduction is small,

${ [g^{(k)}]^' [G^{(k)}]^{-1} g^{(k)} \over \max(| f(x^{(k)})|,FSIZE) } \leq r$

where FSIZE is defined by the FSIZE= option. For the CONGRA technique (where a reliable Hessian estimate G is not available),

${ \parallel g^{(k)} \parallel_2^2 \parallel s^{(k)} \parallel_2 \over \parallel g^{(k)} - g^{(k-1)} \parallel_2 \max(| f(x^{(k)})|,FSIZE) } \leq r$

is used. The default value is r=1E-8. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

Note:: The default setting for the GCONV= option sometimes leads to early termination far from the location of the optimum. This is especially true for the special form of this criterion used in the CONGRA optimization.

GCONV2 | GTOL2=r <n>

specifies another relative gradient convergence criterion. For least-squares problems and the TRUREG, LEVMAR, NRRIDG, and NEWRAP techniques, the criterion of Browne (1982) is used,

$\max_j {| g_j^{(k)}| \over \sqrt{f(x^{(k)})G_{j,j}^{(k)}} } \leq r$

This criterion is not used by the other techniques. The default value is r=0. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

XCONV | XTOL=r <n>

specifies the relative parameter convergence criterion. Termination requires a small relative parameter change in subsequent iterations,

${\max_j | x_j^{(k)} - x_j^{(k-1)}| \over \max(| x_j^{(k)}|,| x_j^{(k-1)}|,XSIZE)} \leq r$

The default value is r=0. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

XSIZE=r

specifies the XSIZE parameter of the relative function and relative gradient termination criteria. The default value is r=0. See the XCONV= option.

Options for Nonlinearly Constrained Techniques

The non-NMSIMP algorithms available for nonlinearly constrained optimization (currently only TECH=QUANEW) do not monotonically reduce either the value of the objective function or some kind of merit function that combines objective and constraint functions. Furthermore, the algorithm uses the watchdog technique with backtracking (Chamberlain et al., 1982). Therefore, no termination criteria are implemented that are based on the values (x or f) of successive iterations. In addition to the criteria used by all optimization techniques, only three more termination criteria are currently available, and they are based on the Lagrange function

$L(x,\lambda) = f(x) - \sum_{i=1}^m \lambda_i c_i(x)$

and its gradient

$\nabla_x L(x,\lambda) = g(x) - \sum_{i=1}^m \lambda_i \nabla_x c_i(x)$

Here, m denotes the total number of constraints, g=g(x) denotes the gradient of the objective function, and $\lambda$ denotes the m vector of Lagrange multipliers. The Kuhn-Tucker conditions require that the gradient of the Lagrange function is zero at the optimal point $(x^*,\lambda^*)$ :

$\nabla_x L(x^*,\lambda^*) = 0$

The termination criteria available for nonlinearly constrained optimization follow.

ABSGCONV | ABSGTOL=r <n>

specifies that termination requires the maximum absolute gradient element of the Lagrange function to be small,

$\max_j | \{\nabla_x L(x^{(k)},\lambda^{(k)})\}_j | \leq r$

The default value is r=1E-5. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

FCONV2 | FTOL2=r <n>

specifies that termination requires the predicted objective function reduction to be small:

$| g(x^{(k)}) s(x^{(k)})| + \sum_{i=1}^m |\lambda_i c_i| \leq r$

The default value is r=1E-6. This is the criterion used by the programs VMCWD and VF02AD (Powell 1982b). The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

GCONV | GTOL=r <n>

specifies that termination requires the normalized predicted objective function reduction to be small:

${ { | g(x^{(k)}) s(x^{(k)})| + \sum_{i=1}^m |\lambda_i c_i(x^{(k)})| } \over { \max(| f(x^{(k)})|,FSIZE) } } \leq r$

where FSIZE is defined by the FSIZE= option. The default value is r=1E-8. The optional integer value n determines the number of successive iterations for which the criterion must be satisfied before the process can be terminated.

Miscellaneous Options

Options for the Approximate Covariance Matrix of Parameter Estimates

You can specify the following options to modify the approximate covariance matrix of parameter estimates.

CFACTOR=r: specifies the scalar factor for the covariance matrix of parameter estimates. The scalar $r \geq 0$ replaces the default value c/NM. For more details, see the section "Approximate Standard Errors".
NOHLF: specifies that the Hessian matrix of the objective function (rather than the Hessian matrix of the Lagrange function) is used for computing the approximate covariance matrix of parameter estimates and, therefore, the approximate standard errors.

It is theoretically not correct to use the NOHLF option. However, since most implementations use the Hessian matrix of the objective function and not the Hessian matrix of the Lagrange function for computing approximate standard errors, the NOHLF option can be used to compare the results.

Options for Additional Displayed Output

You can specify the following options to obtain additional displayed output.

PALL | ALL: displays information on the starting values and final values of the optimization process.
PCRPJAC | PJTJ: displays the approximate Hessian matrix. If general linear or nonlinear constraints are active at the solution, the projected approximate Hessian matrix is also displayed.
PHESSIAN | PHES: displays the Hessian matrix. If general linear or nonlinear constraints are active at the solution, the projected Hessian matrix is also displayed.
PHISTORY | PHIS: displays the optimization history. The PHISTORY option is set automatically if the PALL or PRINT option is set.
PINIT | PIN: displays the initial values and derivatives (if available). The PINIT option is set automatically if the PALL option is set.
PNLCJAC: displays the Jacobian matrix of nonlinear constraints specified by the NLINCON statement. The PNLCJAC option is set automatically if the PALL option is set.
PRINT | PRI: displays the results of the optimization process, such as parameter estimates and constraints.

More Options for Optimization Techniques

You can specify the following options, in addition to the options already listed, to fine-tune the optimization process. These options should not be necessary in most applications of PROC CALIS.

DAMPSTEP | DS <=r>

specifies that the initial step-size value $\alpha^{(0)}$ for each line search (used by the QUANEW, CONGRA, or NEWRAP techniques) cannot be larger than r times the step-size value used in the former iteration. If the factor r is not specified, the default value is r=2. The DAMPSTEP option can prevent the line-search algorithm from repeatedly stepping into regions where some objective functions are difficult to compute or where they can lead to floating point overflows during the computation of objective functions and their derivatives. The DAMPSTEP<=r> option can prevent time-costly function calls during line searches with very small step sizes $\alpha$ of objective functions. For more information on setting the start values of each line search, see the section "Restricting the Step Length".

HESCAL | HS = 0 | 1 | 2 | 3

specifies the scaling version of the Hessian or crossproduct Jacobian matrix used in NRRIDG, TRUREG, LEVMAR, NEWRAP, or DBLDOG optimization. If HS is not equal to zero, the first iteration and each restart iteration sets the diagonal scaling matrix D⁽⁰⁾ = diag(d_i⁽⁰⁾):

$d_i^{(0)} = \sqrt{\max(|{G}^{(0)}_{i,i}|,\epsilon)}$

where G⁽⁰⁾_i,i are the diagonal elements of the Hessian or crossproduct Jacobian matrix. In every other iteration, the diagonal scaling matrix D⁽⁰⁾ = diag(d_i⁽⁰⁾) is updated depending on the HS option:

HS=0

specifies that no scaling is done.

HS=1

specifies the Mor $\acute{e}$ (1978) scaling update:

$d_i^{(k+1)} = \max(d_i^{(k)}, \sqrt{\max(|{G}^{(k)}_{i,i}|,\epsilon)})$

HS=2

specifies the Dennis, Gay, and Welsch (1981) scaling update:

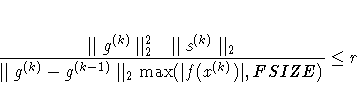
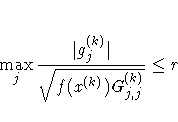
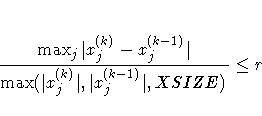
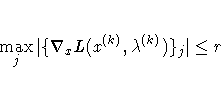
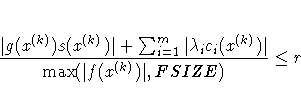
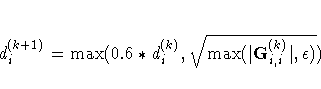
$d_i^{(k+1)} = \max(0.6 * d_i^{(k)}, \sqrt{\max(|{G}^{(k)}_{i,i}|,\epsilon)})$

HS=3

specifies that d_i is reset in each iteration:

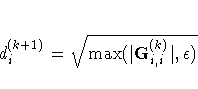
$d_i^{(k+1)} = \sqrt{\max(|{G}^{(k)}_{i,i}|,\epsilon)}$

In the preceding equations, $\epsilon$ is the relative machine precision. The default is HS=1 for LEVMAR minimization and HS=0 otherwise. Scaling of the Hessian or crossproduct Jacobian can be time-consuming in the case where general linear constraints are active.

LCDEACT | LCD = r

specifies a threshold r for the Lagrange multiplier that decides whether an active inequality constraint remains active or can be deactivated. For maximization, r must be greater than zero; for minimization, r must be smaller than zero. The default is

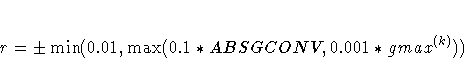
$r = +- \min(0.01, \max(0.1 * ABSGCONV,0.001 * gmax^{(k)}))$

where "+" stands for maximization, "-" stands for minimization, ABSGCONV is the value of the absolute gradient criterion, and gmax^(k) is the maximum absolute element of the (projected) gradient g^(k) or Z'g^(k).

LCEPSILON | LCEPS | LCE = r

specifies the range r, $r \geq 0$ ,for active and violated boundary and linear constraints. If the point x^(k) satisfies the condition

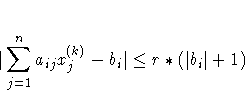
$| \sum_{j=1}^n a_{ij} x_j^{(k)} - b_i | \leq r * (| b_i| + 1)$

the constraint i is recognized as an active constraint. Otherwise, the constraint i is either an inactive inequality or a violated inequality or equality constraint. The default value is r=1E-8. During the optimization process, the introduction of rounding errors can force PROC NLP to increase the value of r by factors of 10. If this happens, it is indicated by a message displayed in the log.

LCSINGULAR | LCSING | LCS = r

specifies a criterion r, $r \geq 0$ , used in the update of the QR decomposition that decides whether an active constraint is linearly dependent on a set of other active constraints. The default is r=1E-8. The larger r becomes, the more the active constraints are recognized as being linearly dependent.

NOEIGNUM

suppresses the computation and displayed output of the determinant and the inertia of the Hessian, crossproduct Jacobian, and covariance matrices. The inertia of a symmetric matrix are the numbers of negative, positive, and zero eigenvalues. For large applications, the NOEIGNUM option can save computer time.

RESTART | REST = i

specifies that the QUANEW or CONGRA algorithm is restarted with a steepest descent/ascent search direction after at most i iterations, i>0. Default values are as follows:

CONGRA: UPDATE=PB: restart is done automatically so specification of i is not used.
CONGRA: UPDATE $\neq$ PB: i = min(10n,80), where n is the number of parameters.
QUANEW: i is the largest integer available.

VERSION | VS = 1 | 2

specifies the version of the quasi-Newton optimization technique with nonlinear constraints.

VS=1: specifies the update of the $\mu$ vector as in Powell (1978a, 1978b) (update like VF02AD).
VS=2: specifies the update of the $\mu$ vector as in Powell (1982a, 1982b) (update like VMCWD).

The default is VS=2.

Chapter Contents
Previous
Next
Top