STAT 350: Lecture 33

Theory of Generalized Linear Models

If Y has a Poisson distribution with parameter then

for k a non-negative integer. We can use the method of maximum likelihood to estimate k if we have a sample of independent Poisson random variables all with mean . If we observe , and so on then the likelihood function is

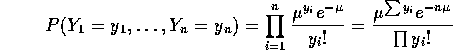
This function of can be maximized by maximizing its logarithm, the log likelihood function. We set the derivative of the log likelihood with respect to equal to 0, getting

This is the likelihood equation and its solution is the maximum likelihood estimate of .

In a regression problem all the will have different means . Our log-likelihood is now

If we treat all n of the we can maximize the log likelihood by setting each of the n partial derivatives with respect to for k from 1 to n equal to 0. The kth of these n equations is just

This leads to . In glm jargon this model is the saturated model.

A more useful model is one in which there are fewer parameters but more than 1. A typical glm model is

where the are covariate values for the ith observation (often including an intercept term just as in standard linear regression).

In this case the log-likelihood is

which should be treated as a function of and maximized.

The derivative of this log-likelihood with respect to is

If has p components then setting these p derivatives equal to 0 gives the likelihood equations.

It is no longer possible to solve the likelihood equations analytically. We have, instead, to settle for numerical techniques. One common technique is called iteratively re-weighted least squares. For a Poisson variable with mean the variance is . Ignore for a moment the fact that if we knew we would know and consider fitting our model by least squares with the known. We would minimize (see our discussion of weighted least squares)

by taking the derivative with respect to and (again ignoring the fact that depends on we would get

But the derivative of with respect to is and replacing by we get the equation

exactly as before. This motivates the following estimation scheme.

1. Begin with a guess for the standard deviations (taking them all equal to 1 is simple).
2. Do (non-linear) weighted least squares using the guessed weights. Get estimated regression parameters .
3. Use these to compute estimated variances . Go back to do weighted least squares with these weights.
4. Iterate (repeat over and over) until estimates not really changing.

Non-linear least squares

In a regression model of the form

we call the model linear if for some covariates and a parameter . Often, however, we have non-linear models such as or in general for some function f which need not be linear in . If the errors are homo-scedastic normal errors then the maximum likelihood estimates of the are least squares estimates, minimizing . The value then solves

This equation can usually not be solved analytically. In general the process of solving it numerically is iterative. One approach is:

1. Begin with an initial guess (no general method available to do this step) for the parameter estimates, say .
2. Linearize the function around by doing a Taylor expansion. This involves writing

   

   where is the vector of partial derivatives of with respect to the entries in .

3. Replace in the sum of squares by this approximation and get that you are trying to minimize

   

   with respect to .

4. This is really now an ordinary least squares problem in which we are regressing on . Let be the matrix with ith row where the derivative is evaluated at . Then we are to minimize

   

   where . The solution is . We compute this .

5. Update to .
6. Recompute the entries in X with the new value , get a new then a and so on.
7. Continue until the estimates change little or the sum of squares changes little.

Example

In thermoluminescence dating ( see Lecture 1) a common model is

Thus in this case

The derivatives of with respect to the entries of are

and

Software and computing details

In SAS the procedure proc nlin will do non-linear least squares. You need to specify quite a few ingredients. The model statement must specify the exact functional form of the function . You have a statement parms which is needed to specify the initial guess for . You usually will have a bunch of der statements to specify derivatives of the predicted values with respect to each parameter and, if you use some algorithms, you will even specify some second derivatives. (You get a choice of 5 different iterative algorithms. The one described above is called Gauss-Newton.)

In Splus the function nls can be used to to the same thing.