NLPDD Call

Language Reference

NLPDD Call

nonlinear optimization by double dogleg method

CALL NLPDD( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit", "grd">);

See "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11, "Nonlinear Optimization Examples," for a description of the inputs to and outputs of all NLP subroutines.

The double dogleg optimization method combines the ideas of the quasi-Newton and trust-region methods. In each iteration, the algorithm computes the step, s^(k), as a linear combination of the steepest descent or ascent search direction, s₁^(k), and a quasi-Newton search direction, s₂^(k), as follows:

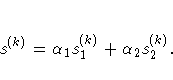
$s^{(k)} = \alpha_1 s_1^{(k)} + \alpha_2 s_2^{(k)} .$

The step s^(k) must remain within a specified trust-region radius (refer to Fletcher 1987). Hence, the NLPDD subroutine uses the dual quasi-Newton update but does not perform a line search. You can specify one of two update formulas with the fourth element of the opt input argument.

Value of opt[4] Update Method

1 Dual BFGS update of the Cholesky factor of the Hessian matrix.

This is the default.

2 Dual DFP update of the Cholesky factor of the Hessian matrix

The double dogleg optimization technique works well for medium to moderately large optimization problems, in which the objective function and the gradient are much faster to compute than the Hessian. The implementation is based on Dennis and Mei (1979) and Gay (1983), but it is extended for boundary and linear constraints. The NLPDD subroutine generally needs more iterations than the techniques that require second-order derivatives (NLPTR, NLPNRA, and NLPNRR), but each of the NLPDD iterations is computationally inexpensive. Furthermore, the NLPDD subroutine needs only gradient calls to update the Cholesky factor of an approximate Hessian.

In addition to the standard iteration history, the NLPDD routine prints the following information:

The heading lambda refers to the parameter $\lambda$ of the double dogleg step. A value of 0 corresponds to the full (quasi-) Newton step.
The heading slope refers to g^Ts, the slope of the search direction at the current parameter iterate x^(k). For minimization, this value should be significantly smaller than zero.

The following statements invoke the NLPDD subroutine to solve the constrained Betts optimization problem (see "Constrained Betts Function" ). The iteration history is shown in Figure 17.1.

   proc iml;
      start F_BETTS(x);
         f = .01 * x[1] * x[1] + x[2] * x[2] - 100.;
         return(f);
      finish F_BETTS;

      con = {  2. -50.  .   .,
              50.  50.  .   .,
              10.  -1. 1. 10.};
      x = {-1. -1.};
      optn = {0 1};
      call nlpdd(rc,xres,"F_BETTS",x,optn,con);
      quit;

                        Double Dogleg Optimization

        Dual Broyden - Fletcher - Goldfarb - Shanno Update (DBFGS)

                        Without Parameter Scaling
                 Gradient Computed by Finite Differences

                   Parameter Estimates               2
                   Lower Bounds                      2
                   Upper Bounds                      2
                   Linear Constraints                1

                         Optimization Start

Active Constraints            0  Objective Function     -98.5376
Max Abs Gradient Element      2  Radius                        1


                                                             
                    Function        Active       Objective    
 Iter    Restarts      Calls   Constraints        Function      

    1           0          2             0       -99.54678     
    2           0          3             0       -99.59120     
    3           0          5             0       -99.90252     
    4           0          6             1       -99.96000      
    5           0          7             1       -99.96000     
    6           0          8             1       -99.96000    


              Objective    Max Abs              Slope of
               Function   Gradient                Search
  Iter           Change    Element    Lambda   Direction

     1           1.0092     0.1346     6.012      -1.805
     2           0.0444     0.1279         0     -0.0228
     3           0.3113     0.0624         0      -0.209
     4           0.0575    0.00432         0     -0.0975
     5          4.66E-6   0.000079         0     -458E-8
     6         1.559E-9          0         0     -16E-10


                           Optimization Results

Iterations                              6  Function Calls                9
Gradient Calls                          8  Active Constraints            1
Objective Function                 -99.96  Max Abs Gradient Element      0                    
Slope of Search Direction     -1.56621E-9  Radius                        1                    


   GCONV convergence criterion satisfied.

Figure 17.1: Iteration History for the NLPDD Subroutine

Chapter Contents
Previous
Next
Top

*Value of opt[4]*	Update Method
1	Dual BFGS update of the Cholesky factor of the Hessian matrix.
	This is the default.
2	Dual DFP update of the Cholesky factor of the Hessian matrix