NLPQN Call

Chapter Contents

Language Reference

NLPQN Call

nonlinear optimization by quasi-Newton method

CALL NLPQN( rc, xr, "fun", x0 <,opt, blc, tc, par, "ptit",

"grd", "nlc", "jacnlc">);

See "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines. See Chapter 11, "Nonlinear Optimization Examples," for a description of the inputs to and outputs of all NLP subroutines.

The NLPQN subroutine uses (dual) quasi-Newton optimization techniques, and it is one of the two subroutines available that can solve problems with nonlinear constraints. These techniques work well for medium to moderately large optimization problems where the objective function and the gradient are much faster to compute than the Hessian matrix. The NLPQN subroutine does not need to compute second-order derivatives, but it generally requires more iterations than the techniques that compute second-order derivatives.

The two categories of problems solved by the NLPQN subroutine are unconstrained or linearly constrained problems and nonlinearly constrained problems. Unconstrained or linearly constrained problems do not use the "nlc" or "jacnlc" module arguments, whereas nonlinearly constrained problems use the arguments to specify the nonlinear constraints and the Jacobian matrix of their first-order derivatives, respectively.

The type of optimization problem specified determines the algorithm that the subroutine invokes. The algorithms are very different, and they use different sets of termination criteria. For more details, see "Termination Criteria"

Unconstrained or Linearly Constrained QN Optimization

The NLPQN subroutine invokes this algorithm if you do not specify the "nlc" argument. Using the fourth element of the opt argument, you can specify two update formulas for either the original quasi-Newton algorithm or the dual quasi-Newton algorithm, as indicated in the following table:

*Value of opt[4]*	Update Method
1	Dual Broyden, Fletcher, Goldfarb, and Shanno (DBFGS) update of the Cholesky factor of the Hessian matrix. This is the default.
2	Dual Davidon, Fletcher, and Powell (DDFP) update of the Cholesky factor of the Hessian matrix.
3	Original Broyden, Fletcher, Goldfarb, and Shanno (BFGS) update of the inverse Hessian matrix.
4	Original Davidon, Fletcher, and Powell (DFP) update of the inverse Hessian matrix.

In each iteration, a line search is performed along the search direction to find an approximate optimum of the objective function. The default line-search method uses quadratic interpolation and cubic extrapolation to obtain a step size that satisfies the Goldstein conditions. One of the Goldstein conditions can be violated if the feasible region defines an upper limit of the step size. Violating the left-side Goldstein condition can affect the positive definiteness of the quasi-Newton update. In these cases, either the update is skipped or the iterations are restarted with an identity matrix resulting in the steepest descent or ascent search direction. You can specify line-search algorithms different from the default method with the fifth element of the opt argument.

Note: In Release 6.08, the DBFGS and DDFP updates were implemented with the NLPDQN subroutine. In Release 6.09 and in later releases, these updates are specified with the NLPQN subroutine, and the NLPDQN subroutine is not permitted.

The following statements invoke the NLPQN subroutine to solve the Rosenbrock problem (see "Unconstrained Rosenbrock Function" ):

   proc iml;
      start F_ROSEN(x);
         y1 = 10. * (x[2] - x[1] * x[1]);
         y2 = 1. - x[1];
         f  = .5 * (y1 * y1 + y2 * y2);
         return(f);
      finish F_ROSEN;
      x = {-1.2 1.};
      optn = {0 2 . 2};
      call nlpqn(rc,xr,"F_ROSEN",x,optn);
      quit;

Since OPTN[4]=2, the DDFP update is performed. The gradient is approximated by finite differences since no module is specified that computes the first-order derivatives. Part of the iteration history is shown in Figure 17.9. In addition to the standard iteration history, the NLPQN subroutine prints the following information for unconstrained or linearly constrained problems:

The heading alpha is the step size, $\alpha$ , computed with the line-search algorithm.
The heading slope refers to g^Ts, the slope of the search direction at the current parameter iterate x^(k). For minimization, this value should be significantly smaller than zero. Otherwise, the line-search algorithm has difficulty reducing the function value sufficiently.

               
                 Optimization Start
                 Parameter Estimates

                                      Gradient
                                      Objective
  N Parameter         Estimate        Function

  1 X1               -1.200000     -107.799989
  2 X2                1.000000      -43.999999

            Value of Objective Function = 12.1


              Dual Quasi-Newton Optimization

     Dual Davidon - Fletcher - Powell Update (DDFP)
      Gradient Computed by Finite Differences

        Parameter Estimates               2

                  Optimization Start

Active Constraints                   0  Objective Function  12.1
Max Abs Gradient Element  107.79998927


                                                            
                    Function        Active       Objective   
 Iter    Restarts      Calls   Constraints        Function    

    1           0          4             0         2.06405    
    2           0          7             0         1.92035     
    3           0         10             0         1.78089     
    4           0         13             0         1.33331    
    5           0         17             0         1.13400     
    6           0         22             0         0.93915    
    7           0         24             0         0.84821    
    8           0         30             0         0.54334     
    9           0         32             0         0.46593   
   10           0         37             0         0.35322      
   12           0         41             0         0.20282     
   12           0         41             0         0.20282     
   13           0         46             0         0.11714     
   14           0         51             0         0.07149    
   15           0         53             0         0.04746     
   16           0         58             0         0.02759     
   17           0         60             0         0.01625      
   18           0         62             0         0.00475    
   19           0         66             0         0.00167    
   20           0         70             0       0.0005952    
   21           0         72             0       0.0000771   
   23           0         78             0      2.39914E-8   
   23           0         78             0      2.39914E-8    
   24           0         80             0      5.0936E-11    
   25           0        119             0      3.9538E-11   



        Objective    Max Abs              Slope of
         Function   Gradient      Step      Search
 Iter      Change    Element      Size   Direction

    1     10.0359     0.7917    0.0340      -628.8
    2      0.1437     8.6301     6.557     -0.0363
    3      0.1395    11.0943     8.193     -0.0288
    4      0.4476     7.6069    33.376     -0.0269
    5      0.1993     0.9386    15.438     -0.0260
    6      0.1948     3.5290    11.537     -0.0233
    7      0.0909     4.8308     8.124     -0.0193
    8      0.3049     4.1770    35.143     -0.0186
    9      0.0774     0.9479     8.708     -0.0178
   10      0.1127     2.5981    10.964     -0.0147
   11      0.0894     3.3028    13.590     -0.0121
   12      0.0610     0.6451    10.000     -0.0116
   13      0.0857     1.6603    11.395     -0.0102
   14      0.0456     2.4050    11.559     -0.0074
   15      0.0240     0.5628     6.868     -0.0071
   16      0.0199     1.3282     5.365     -0.0055
   17      0.0113     1.9246     5.882     -0.0035
   18      0.0115     0.6357     8.068     -0.0032
   19     0.00307     0.4810     2.336     -0.0022
   20     0.00108     0.6043     3.287     -0.0006
   21    0.000518     0.0289     2.329     -0.0004
   22    0.000075     0.0365     1.772     -0.0001
   23    1.897E-6    0.00158     1.159     -331E-8
   24    2.394E-8   0.000016     0.967      -46E-9
   25    1.14E-11   7.962E-7     1.061     -19E-13



              Optimization Results

Iterations                           25  Function Calls                     120
Gradient Calls                      107  Active Constraints                   0
Objective Function         3.953804E-11  Max Abs Gradient Element  7.9622469E-7
Slope of Search Direction  -1.88032E-12


   ABSGCONV convergence criterion satisfied.


               Optimization Results
               Parameter Estimates

                                      Gradient
                                      Objective
  N Parameter         Estimate        Function

  1 X1                0.999991    -0.000000796
  2 X2                0.999982     0.000000430

       Value of Objective Function = 3.953804E-11

Figure 17.9: Iteration History for the NLPQN Subroutine

Nonlinearly Constrained QN Optimization

The algorithm used for nonlinearly constrained quasi-Newton optimization is an efficient modification of Powell's (1978, 1982) Variable Metric Constrained WatchDog (VMCWD) algorithm. A similar but older algorithm (VF02AD) is part of the Harwell library. Both the VMCWD and VF02AD algorithms use Fletcher's VE02AD algorithm, which is also part of the Harwell library, for positive definite quadratic programming. This NLPQN implementation uses a quadratic programming subroutine that updates and downdates the Cholesky factor when the active set changes (refer to Gill, Murray, Saunders, and Wright 1984). The nonlinear NLPQN algorithm is not a feasible point algorithm, and the value of the objective function is not required to decrease monotonically. Instead, the algorithm tries to reduce a linear combination of objective function and constraint violations. The following are similarities and differences between this algorithm and Powell's VMCWD algorithm:

You can use the sixth element of the opt argument to modify the algorithm used by the NLPQN subroutine. If you specify opt[6]=2, which is the default, the evaluation of the Lagrange vector $\mu$ is performed the same way as described in Powell (1982b). Note, however, that the VMCWD program seems to have a bug in the implementation of formula (4.4) in Powell (1982b). If you specify opt[6]=1, the original update of $\mu$ used in the VF02AD algorithm in Powell (1978a) is performed.
Instead of updating an approximate Hessian matrix, this algorithm uses the dual BFGS or dual DFP update that updates the Cholesky factor of an approximate Hessian. If the condition of the updated matrix gets too bad, a restart is done with a positive diagonal matrix. At the end of the first iteration after each restart, the Cholesky factor is scaled.
The Cholesky factor is loaded into the quadratic programming subroutine, which ensures positive definiteness of the problem. During the quadratic programming step, the Cholesky factor of the projected Hessian matrix Z^T_kGZ_k is updated simultaneously with QT decomposition when the active set changes. Refer to Gill, Murray, Saunders, and Wright (1984) for more information.
The line-search strategy is very similar to that of Powell's algorithm, but this algorithm does not call for derivatives during the line search. For that reason, this algorithm generally needs fewer derivative calls than function calls, whereas the VMCWD algorithm always requires the same number of derivative calls as function calls. Also, Powell's line-search method sometimes uses steps that are too long during the early iterations. In those cases, you can use the second element of the par argument to restrict the step length $\alpha$ in the first five iterations. See "Control Parameters Vector" for more details.
The watchdog strategy is also similar to that of Powell's algorithm. However, this algorithm does not return automatically after a fixed number of iterations to a previous, more optimal point. A return to such a point is further delayed if the observed function reduction is close to the expected function reduction of the quadratic model.
Although Powell's termination criterion, the FTOL2 criterion, can still be used, the NLPQN implementation uses, by default, two other termination criteria (GTOL and ABSGTOL).

This algorithm is automatically invoked if the "nlc" argument is specified. The module specified with the "nlc" argument must return a vector of length nc, where nc is the total number of constraints. Letting nec be the number of equality constraints, the constraints must be of the following form:

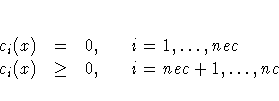
$c_i(x) & = & 0, & & i=1, ... ,nec \c_i(x) & \geq & 0, & & i=nec+1, ... ,nc$

The first nec elements of the returned vector contain the c_i for the equality constraints, and the remaining elements contain the c_i for the inequality constraints.

Note: You must specify the total number of constraints with the tenth element of the opt argument, and if there are any equality constraints, you must specify that number, nec, with the eleventh element of the opt argument. The nonlinear NLPQN algorithm requires the Jacobian matrix of the first-order derivatives of the nc constraints returned by the module specified by the "nlc" argument. You can provide these derivatives by specifying a module with the "jacnlc" argument. This module must return the Jacobian matrix J of first-order partial derivatives. That is, J is an nc ×n matrix such that the entry in the i^th row and j^th column is given by

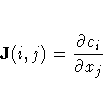
$J(i,j) = \frac{\partial c_i}{\partial x_j}$

If you specify an "nlc" module without specifying a "jacnlc" argument, finite difference approximations of the first-order derivatives of the constraints are used. You can use the ninth element of the par argument to specify the number of accurate digits used in evaluating the constraints.

You can specify two update formulas with the fourth element of the opt argument as indicated in the following table:

Value of opt[4] Update Method

1 Dual Broyden, Fletcher, Goldfarb, and Shanno (DBFGS) update of the Cholesky factor of the Hessian matrix. This is the default.

2 Dual Davidon, Fletcher, and Powell (DDFP) update of the Cholesky factor of the Hessian matrix.

This algorithm uses its own line-search technique. None of the options and parameters that control the line search in the other algorithms apply in the nonlinear NLPQN algorithm, with the exception of the second element of the par vector, which can be used to restrict the length of the step size in the first five iterations.

See Example 11.8 for an example where you need to specify a value for the second element of the par argument. The values of the fourth, fifth, and sixth elements of the par vector, which control the processing of linear and boundary constraints, are valid only for the quadratic programming subroutine used in each iteration of the NLPQN call. For a simple example of the NLPQN subroutine, see "Rosen-Suzuki Problem" .

Chapter Contents
Previous
Next
Top