Constructing Box Charts

BOXCHART Statement

Constructing Box Charts

The following notation is used in this section:

$\mu$ process mean (expected value of the population of measurements)

$\sigma$ process standard deviation (standard deviation of the population of measurements)

$\bar{X}_{i}$ mean of measurements in i^th subgroup

n_i sample size of i^th subgroup

N the number of subgroups

x_ij j^th measurement in the i^th subgroup, j = 1,2,3 ... , n_i

x_i(j) j^th largest measurement in the i^th subgroup:
$x_{i(1)} \leq x_{i(2)} \leq ... \leq x_{i(n_{i})}$

$\overline{\overline{X}}$ weighted average of subgroup means

M_i median of the measurements in the i^th subgroup:
$M_i = \{ x_{i((n_i + 1)/2)} & {if n_{i} is odd} \ (x_{i(n_i/2)} + x_{i((n_i/2)+1)})/2 & {if n_{i} is even} .$

$\bar{M}$ average of the subgroup medians:
$\bar{M} = (n_1M_1 + ... + n_NM_N)/(n_1+ ... +n_N)$

$\tilde{M}$ median of the subgroup medians. Denote the j^th largest median by M_(j) so that $M_{(1)} \leq M_{(2)}\leq ... \leq M_{(N)}$ .
$\tilde{M} = \{ M_{((N+1)/2)} & {if N is odd} \ (M_{(N/2)} + M_{(N/2)+1})/2 & {if N is even} .$

e_M(n) standard error of the median of n independent, normally distributed variables with unit standard deviation (the value of e_M(n) can be calculated with the STDMED function in a DATA step)

Q_p(n) 100p^th percentile (0<p<1) of the distribution of the median of n independent observations from a normal population with unit standard deviation

z_p 100p^th percentile of the standard normal distribution

D_p(n) 100p^th percentile of the distibution of the range of n independent observations from a normal population with unit standard deviation

Elements of Box-and-Whisker Plots

A box-and-whisker plot is displayed for the measurements in each subgroup on the box chart. Figure 32.12 illustrates the elements of each plot.

Figure 32.12: Box-and-Whisker Plot

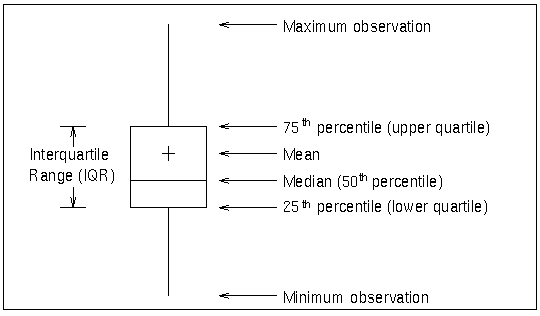
The skeletal style of the box-and-whisker plot shown in Figure 32.12 is the default. You can specify alternative styles with the BOXSTYLE= option; see Example 32.2 or the entry for the BOXSTYLE= option.

Control Limits and Central Line

You can compute the limits in the following ways:

as a specified multiple (k) of the standard error of $\bar{X}_{i}$ (or M_i) above and below the central line. The default limits are computed with k=3 (these are referred to as $3\sigma$ limits).
as probability limits defined in terms of $\alpha$ , a specified probability that $\bar{X}_{i}$ (or M_i) exceeds the limits

The CONTROLSTAT= option specifies whether control limits are computed for subgroup means (the default) or subgroup medians. The following tables provide the formulas for the limits:

Table 32.23: Control Limits and Central Line for Box Charts

CONTROLSTAT=MEAN	CONTROLSTAT=MEDIAN

LCLX = lower limit $= \overline{\overline{X}} - k\hat{\sigma}/ \sqrt{n_{i}}$	LCLM = lower limit $= \bar{M} - k\hat{\sigma}e_{M}(n_i)$
Central Line $= \overline{\overline{X}}$	Central Line $= \bar{M}$
UCLX = upper limit $= \overline{\overline{X}} + k\hat{\sigma}/ \sqrt{n_{i}}$	UCLM = upper limit $= \bar{M} + k\hat{\sigma}e_{M}(n_i)$

Table 32.24: Probability Limits and Central Line for Box Charts

CONTROLSTAT=MEAN	CONTROLSTAT=MEDIAN

LCLX = lower limit $= \overline{\overline{X}} - z_{\alpha/2}(\hat{\sigma}/ \sqrt{n_{i}})$	LCLM = lower limit $= \bar{M} - Q_{\alpha/2}(n_i)\hat{\sigma}$
Central Line $= \overline{\overline{X}}$	Central Line $= \bar{M}$
UCLX = upper limit $= \overline{\overline{X}} + z_{\alpha/2}(\hat{\sigma}/ \sqrt{n_{i}})$	UCLM = upper limit $= \bar{M} + Q_{1-\alpha/2}(n_i)\hat{\sigma}$

In the preceding tables, replace $\bar{M}$ with $\overline{\overline{X}}$ if you specify MEDCENTRAL=AVGMEAN in addition to CONTROLSTAT=MEDIAN. Likewise, replace $\bar{M}$ with $\tilde{M}$ if you specify MEDCENTRAL=MEDMED in addition to CONTROLSTAT=MEDIAN. If standard values $\mu_{0}$ and $\sigma_{0}$ are available for $\mu$ and $\sigma$ , replace $\overline{\overline{X}}$ with $\mu_{0}$ and $\hat{\sigma}$ with $\sigma_{0}$ in Table 32.23 and Table 32.24.

Note that the limits vary with n_i. The formulas for median limits assume that the data are normally distributed.

You can specify parameters for the limits as follows:

Specify k with the SIGMAS= option or with the variable _SIGMAS_ in a LIMITS= data set.
Specify $\alpha$ with the ALPHA= option or with the variable _ALPHA_ in a LIMITS= data set.
Specify a constant nominal sample size $n_{i} \equiv n$ for the control limits with the LIMITN= option or with the variable _LIMITN_ in a LIMITS= data set.
Specify $\mu_{0}$ with the MU0= option or with the variable _MEAN_ in a LIMITS= data set.
Specify $\sigma_{0}$ with the SIGMA0= option or with the variable _STDDEV_ in a LIMITS= data set.

Note: You can suppress the display of the control limits with the NOLIMITS option. This is useful for creating standard side-by-side box-and-whisker plots (in this case, the STDDEVIATIONS option is also recommended).

Chapter Contents
Previous
Next
Top

$\mu$	process mean (expected value of the population of measurements)
$\sigma$	process standard deviation (standard deviation of the population of measurements)
$\bar{X}_{i}$	mean of measurements in i^th subgroup
n_i	sample size of i^th subgroup
N	the number of subgroups
x_ij	j^th measurement in the i^th subgroup, j = 1,2,3 ... , n_i
x_i(j)	j^th largest measurement in the i^th subgroup: $x_{i(1)} \leq x_{i(2)} \leq ... \leq x_{i(n_{i})}$
$\overline{\overline{X}}$	weighted average of subgroup means
M_i	median of the measurements in the i^th subgroup: $M_i = \{ x_{i((n_i + 1)/2)} & {if n_{i} is odd} \ (x_{i(n_i/2)} + x_{i((n_i/2)+1)})/2 & {if n_{i} is even} .$
$\bar{M}$	average of the subgroup medians: $\bar{M} = (n_1M_1 + ... + n_NM_N)/(n_1+ ... +n_N)$
$\tilde{M}$	median of the subgroup medians. Denote the j^th largest median by M_(j) so that $M_{(1)} \leq M_{(2)}\leq ... \leq M_{(N)}$ . $\tilde{M} = \{ M_{((N+1)/2)} & {if N is odd} \ (M_{(N/2)} + M_{(N/2)+1})/2 & {if N is even} .$
e_M(n)	standard error of the median of n independent, normally distributed variables with unit standard deviation (the value of e_M(n) can be calculated with the STDMED function in a DATA step)
Q_p(n)	100p^th percentile (0<p<1) of the distribution of the median of n independent observations from a normal population with unit standard deviation
z_p	100p^th percentile of the standard normal distribution
D_p(n)	100p^th percentile of the distibution of the range of n independent observations from a normal population with unit standard deviation