Hungarian Rings

This puzzle consists of two intersecting rings made up of a number of coloured balls. The rings of balls intersect at two places, so they share two of the balls. Each ring of balls can be rotated, so the balls can be mixed. The aim is to mix up the balls, and then place the balls back together so each colour form a continuous sequence.
The applet below was written by Jaap Scherphuis © ( Jaap's Puzzle Page).
The basic legal moves of the Hungarian Rings puzzle are $R$, and $L$, where $R$ denotes a clockwise rotation of numbers around the right-hand ring (each number moves one space), and $L$ denotes a clockwise rotation of numbers around the left-hand ring.
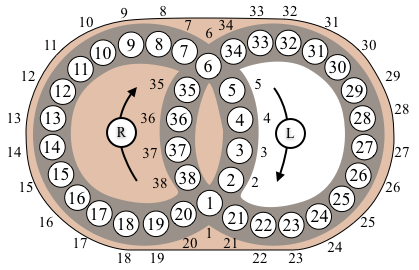
The permutation corresponding to each of the legal moves $R$ and $L$ are: $$\begin{array}{l} R = (1,38,37,36,35,6,34,33,32,31,30,29,28,27,26,25,24,23,22,21)\\ L = (1,20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2) \end{array}$$ $R^{-1}$ and $L^{-1}$ correspond to the inverses of these permutations.
The Hungarian Rings puzzle group $HR$ can be represented as a subgroup of the Symmetric group $S_{38}$ generated by these two permutations. $$HR = \langle R, L \rangle.$$ We can define $HR$ in SageMath as follows.