Rubik's Pocket Cube
The applet below was written by Werner Randelshofer ( CubeTwister).
Since this cube is really just the 3×3×3 Rubik's cube with all the edge pieces removed then our notation, and analysis, of Rubik's cube can be applied to the Pocket cube. To solve this puzzle just apply the basic solution of Rubik's cube and ignore steps involving edge cubies.
There is really only one aspect of the pocket cube that once needs to be careful in dealing with. There are no fixed-centres on this cube, unlike the 3×3×3 cube where each centre cubie remains fixed under face-twists. This means we have to be careful on how we fix an orientation of the cube in space. We'll see below how this affects our representation of the cube as a subgroup of $S_{34}$.
Representing the cube as a subgroup of $S_{24}$
Label the facets of the Rubik's Cube as shown in the diagram.

It may help to view this labeling on the flattened cube as follows.
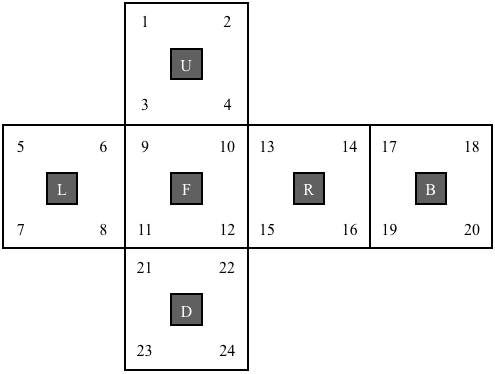
The permutation corresponding to each of the basic moves of the Rubik's Cube are: $$\begin{array}{l} R = (13,14,16,15)(10,2,19,22)(12,4,17,24)\\ L = (5,6,8,7)(3,11,23,18)(1,9,21,20)\\ U = (1,2,4,3)(9,5,17,13)(10,6,18,14)\\ D = (21,22,24,23)(11,15,19,7)(12,16,20,8)\\ F = (9,10,12,11)(3,13,22,8)(4,15,21,6)\\ B = (17,18,20,19)(1,7,24,14)(2,5,23,16)\\ \end{array}$$ $R^{-1}, L^{-1}, U^{-1}, D^{-1}, F^{-1}, B^{-1}$ correspond to the inverses of these permutations.
There is one major difference between the Pocket cube and Rubik's cube: the Pocket cube does not have any fixed centres. Why does this matter? Consider the moves $R$ and $L$. They are equivalent! Notice that applying $R$, leaves the cube in exactly the same position as $L$ (the cube as a whole has just been rotated in space). Another way to say this is $RL^{-1}$ is the identity in the cube group $RC_2$. Try it!
If we were to use the permutations above to generate a group then this wouldn't be the group $RC_2$. Since the product of permutations associated with $R$ and $L$ don't have the property that $RL^{-1}=\varepsilon$. This means the permutations are picking up the fact that the cube rotated in space, even though the cube is in the solved state.
Again let's summarize the real difference between Rubik's cube and the Pocket cube: the Pocket cube can be rotated in space using only puzzle moves (which rotate faces), whereas Rubik's cube cannot be rotated in space using puzzle moves (since centres stay fixed under face rotations).
This means that $RC_2$ is smaller than the permutation group generated by the six permutations above. In fact, we really only need one of each of the following pairs of moves: $\{R,L\}, \{U,D\}, \{F,B\}$. We'll choose to only use $R, D, F$. This means the up-left-back cubie always remains in its home position. This is the piece we will keep fixed, and will be used as our frame of reference.