A Basic 5-Step Solution of Rubik's Cube
It may be surprising to learn that very little memorization is required to solve Rubik's Cube. In fact,
it can be solved using only four types of move sequences:
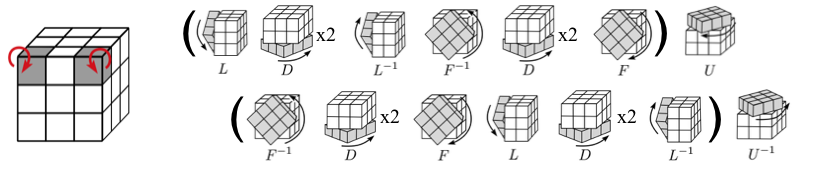
- cycling 3 corner pieces (for permuting corners)
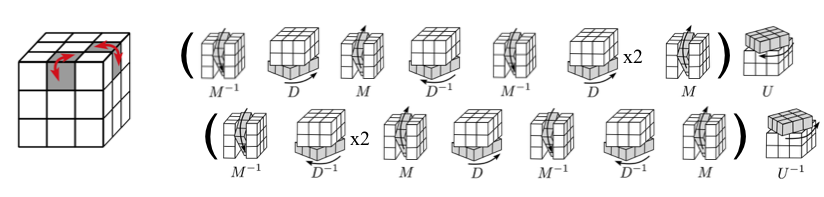
- twisting a pair of corner pieces in opposite directions (for orienting corners)
- cycling 3 edge pieces (for permuting edges)
- flipping a pair of edge pieces (for orienting edges)
For reference, below are the four types of move sequences we'll use to solve the cube (pdf). For most puzzles on this site I would list basic move sequences like the ones below and stop there, leaving it to reader to use them to solve the puzzle. In which case, a video like this one would suffice to demonstrate how to solve the cube. However, some will benefit from a walk-through, so over the next few pages we'll go through the solution and I'll show you how and when to use these sequences.
Corner 3-cycle: (for permuting corners)
Corner twist: (for orienting corners)
Edge 3-cycle: (for permuting edges)
Edge flip: (for orienting edges)
A Note on Commutators
The use of brackets above is to draw your attention to the structure of the sequence, all these move sequences have the same form: $\alpha \beta \alpha^{-1} \beta^{-1}$, where $\alpha$ and $\beta$ are each move sequences themselves. For example, the corner 3-cycle corresponds to $\alpha = L D^{-1}L^{-1}$ and $\beta=U$.
A sequence of the form $\alpha \beta \alpha^{-1} \beta^{-1}$ is called a commutator and is very useful when studying permuations. The following square bracket notation is used as a shorthand: $$[\alpha,\beta]=\alpha \beta \alpha^{-1} \beta^{-1}.$$
Notice that $[\alpha,\beta]^{-1} = [\beta,\alpha]$, which helps when you want to apply the inverse of one of the sequences above. Such as cycling three corners in the opposite direction.
The main point here is that the four move sequences had to be created, and commutators were a natural form to make them since a lot is known about commutators. I won't go into any more details on commutators in this section, but if you want to learn more about commutators see Lecture 13 of the course notes. For a quick look start with this video. This lecture gives you the necessary foundations to build your own move sequences for a variety of other puzzles.
However, in this basic solution I do hope to give you a feel for why commutators are useful, so in steps 4 and 5 I will discuss how these four move sequences were built.
The focus here will be on learning these four types of move sequences listed above, understanding how they work, and how to use them to solve the cube. Let's get started.
For an anatomy lesson of the cube, and an overview of the 5-step solution have a look at this introductory video. (Note: If you are having problems disassembling your cube by popping an edge piece then here is a video that will help.)