The Fundamental Theorem of Cubology

Determining which configurations of the cube are possible.

The Fundamental Theorem of Cubology is a statement that characterizes which configurations are possible, and which configurations are impossible. This theorem underpins our solution strategy, and is the reason we know the four basic moves are enough to solve the puzzle.

We state the Fundamental Theorem in two ways: in a plain language form, then in its more technical group theoretic form.

For example, it is impossible to swap exactly two corner cubies while every other cubie remains in its original position. Such a move would produce an even permutation of the edges (trivial permutation), but an odd permutation of the corners (a 2-cycle). Part (a) of the theorem tells us this is impossible.

---

How to Prove the Fundamental Theorem

Full details are in Chapter 20 of the course text. Only a summary is provided here.

We begin by describing each configuration of the cube in terms where the cubies moved, and how they are oriented when they get there. In particular we represent a configuration by

• a permutation of the 8 corner cubies,
• a permutation of the 12 edge cubies,
• an orientation vector of the 8 corner cubies,
• an orientation vector of the 12 edge cubies.

To do this, consider the puzzle in the solved state and number both the corner and edge cubies as shown in the diagrams. A configuration of the puzzles will therefore produce a permutation on the corners (element of $S_{8}$) and a permutation of the edges (element of $S_{12}$).

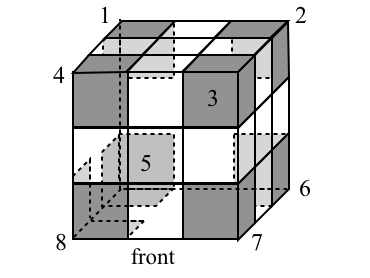
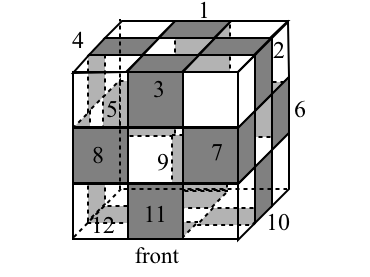
Next, add an orientation mark '+' to each cubicle. This can be done in any number of ways, the only restriction is that each cubicle has only one facet with an orientation mark on it. Think of this marking on the ficticious layer of skin surrounding the cube. The first image below shows our choice of the orientation markings. We call each facet with the '+' marking the primary facet of the cubicle.

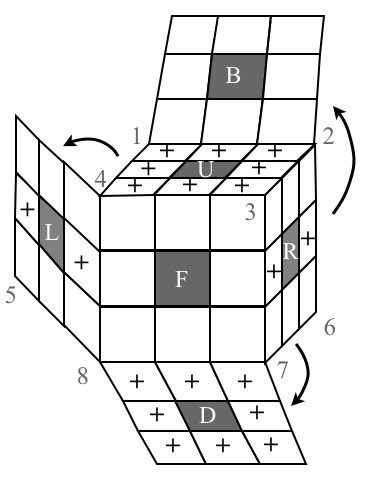
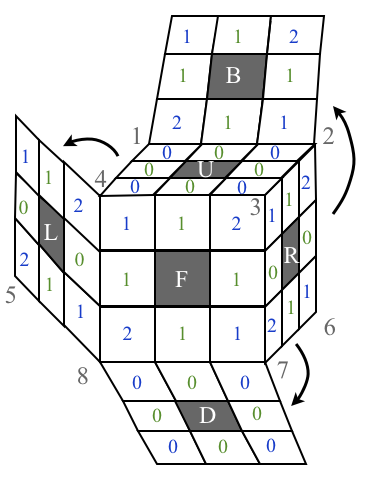
Now mark the stickers on each cubie based on their relative position to the primary facet. For an edge cubie, mark the sticker with a $0$ if it is in the primary facet, and mark the other stricker on the same cubie with a $1$. For a corner cubie, mark the sticker in the primary facet with a $0$, and mark the other two stickers with $1$ and $2$ as you move in the clockwise direction around the cubie. This is shown in the second image above.

It is worth repeating this subtle point, the orientation markings '+' are on the facets which don't move as the faces are twisted. Again, think of these markings on a ficticious layer of skin surronding the cube. The orientation numbers are on the stickers, which do move around as the faces are twisted.

If $X$ is any configuration of Rubik's cube the position vector is a $4$-tuple $(\rho, \sigma, \boldsymbol{v}, \boldsymbol{w})$ where $\rho \in S_{8}$, $\sigma\in S_{12}$ encode the permutations of the cubies, and $\boldsymbol{v}\in \mathbb{Z}_{3}^{8}$ and $\boldsymbol{w} \in \mathbb{Z}_{2}^{12}$ encode the orientations of the cubies:

$\rho\in S_8$	$\rho(i) = j$   if corner cubie $i$ is in cubicle $j$
$\sigma\in S_{12}$	$\sigma(i) = j$   if edge cubie $i$ is in cubicle $j$
$\boldsymbol{v}=(v_1,v_2,\ldots, v_{8}) \in \mathbb{Z}_3^{8}$	$v_i$ is the number on the $i^\text{th}$ corner cubie beneath the '+' mark of the cubicle $\rho(i)$ it occupies.
$\boldsymbol{w}=(w_1,w_2,\ldots, w_{12}) \in \mathbb{Z}_2^{12}$	$w_i$ is the number on the $i^\text{th}$ edge cubie beneath the '+' marking of the cubicle $\sigma(i)$ it occupies.

For example, consider the move $R^{-1}$ which results in the following configuration.

The position vector $(\rho, \sigma, \boldsymbol{v}, \boldsymbol{w})$ for this configuration is:
$\rho = (2,3,7,6)$
$\sigma = (2,7,10,6)$
$\boldsymbol{v} = (0,1,2,0,0,2,1,0)$
$\boldsymbol{w} = (0,1,0,0,0,1,1,0,0,1,0,0).$
In Chapter 20 of the course book you can find the details of this example, and a few more examples where we compute the position vector for a configuration.

Now we can describe the configurations of the cube that are possible in terms of the position vector.

A full proof of this is given in Chapter 20 of the course book. We'll just outline the proof here.

The first thing to show is that the three conditions are necessary, that is, they hold for any legal configuration. To do this we just need to show that if the conditions are satisfied for a configuration, then they also hold for the configuration obtained from it by twising one of the six faces. This involves just looking at the six cases individually.

Next we would need to show that if we had a configuration that satisfies the three conditions then the puzzle is solvable. Here is where our four basic moves come in handy. Let's recall them here for convenience.

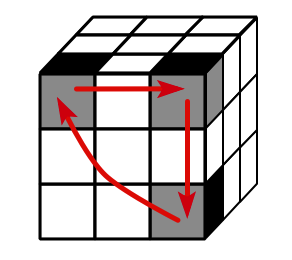
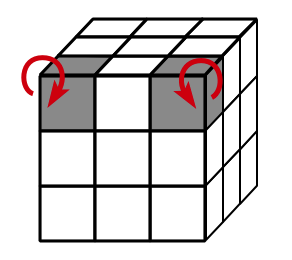
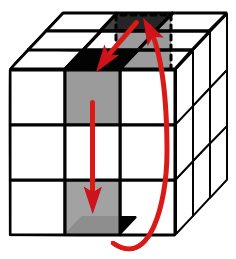
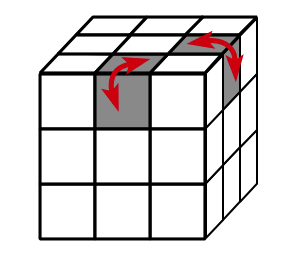
Since the corner and edge permutations have the same parity we can assume they are both even (otherwise twist any random face 90 degrees since this would multiply each by a 4-cycle which is odd). Since the corner permuation is even it is a product of 3-cycles, therefore the corners can be solved using 3-cycles. (We have a 3-cycle move that can be modified to cycle any 3 corner cubies on the puzzle.) Similarly, the edge permutation is even and can be solved using 3-cycles.

Now all cubies are in their correct cubicles. We now have to orient them to solve the puzzle. Condition (b) says that the number of clockwise corner twists is equal to the number of counterclockwise corner twists modulo $3$. So first twist any cw, ccw pairs into their solved positions. The result will be that all remaining corner twists will occur in triples: 3cw or 3ccw. These can be solved using our pairwise corner twisting moves. Finally, condition (c) says an even number of edges will be flipped. Luckily we have a move that will flip them in pairs. Therefore the puzzle can be solved.

Number of Configurations of Rubik's Cube

Full details are in Chapter 20 of the course text. Only a summary is provided here.

The Fundamental Theorem allows us to determine the number of configurations of the cube. First, we start with a much bigger set than just the configurations that are possible to achieve by twisting faces. Consider the set of all possible ways there are to take apart and reassemble the cube. We denote this set by $RC_3^*$ and call it the illegal cube group (sometimes called the assembled cube set). It corresponds to the cartesian product of all possible permuations and orientations: $$RC_3^*= S_{8}\times S_{12} \times \mathbb{Z}_3^{8}\times \mathbb{Z}_{2}^{12}$$ which has size $$|RC_3^*| = 8!\cdot 12! \cdot 3^{8}\cdot 2^{12}.$$ The legal positions $RC_3$ are a subset $RC_3^*$ in which

• $1/2$ the permutations of the edges and corners are possible (parity condition from (a)),
• $1/2$ the orientations of the edges are possible (parity condition (c)),
• $1/3$ of the corner orientations are possible (condition (b)).

This shows the following.