Skip to main content

Section 4.1 Small Number and the Skateboard Park - Classroom Guide

View the full story: Small Number and the Skateboard Park

Suggested Grades: 4 - 7

Subsection 4.1.1 Mathematics

  1. geometry - shapes, patterns, angles
  2. geometrical construction
  3. mathematics and sports
  4. mathematical thinking
  5. mathematics and physics

Subsection 4.1.2 Mathematical Vocabulary

  • small, number, a lot of, big, every, math homework, geometry problem, full angle, walks through, against, geometry, around, shapes, geometric shapes and patterns, geometer, perfect number, 360°, 720°, two ramps, same height, different shapes, flat, curved, inside of a cylinder, a lot of speed, front, spins around fully two times, jumping up and down

Subsection 4.1.3 Cultural Components

  1. Indigenous:
    1. Learn more about a young skateboarder named Suan Campbell of the Ahousaht Nation who was chosen to represent his Nation at the 14th Annual All Nations Skate Jam.
    2. Learn more about Aboriginal Friendship Centres.
    3. Totem poles: Draw and describe a totem pole that you’ve recently seen. Learn more about traditional totem poles. You may start with the SFU Museum of Archeology: Building a totem pole.
    4. Learn more about the Indigenous tradition of weaving. For example. look at this SFU Museum of Anthropology website.
  2. General:
    1. Learn more about Euclid - Wikipedia, the father of geometry.
    2. Learn more about geometrical shapes - Wikipedia.
    3. Do you have a skateboard? Do you know how to skateboard?
    4. Learn more about the different types of ramps that skateboarders use.
    5. Learn more about skateboarding and physics.
    6. Learn about Annie Guglia, a Canadian skateboarding olympian.
    7. Learn more why a full circle is associated with the measurement of 360°.

Subsection 4.1.4 Mathematical Observations (Video)

Click here to see the film (English)

Opening scene: Notice the various shapes, such as: buildings, mountain peaks, wooden structures. Notice the perspective.

0:09 - Notice the various shapes, parallel lines, a sphere, patterns on the totem pole, the symmetry of the totem pole. How many windows are there?

0:16 - Notice the shapes, patterns, perspective, parallel lines, right angles, tiling, shapes and patterns on the rug.

0:43 - Notice the image on Full Angle’s shirt and the skateboard; observe the central symmetry. Notice the shape of the skateboard, the shape of the helmet, and the perspective.

0:51 - Do the images on the rug and Full Angle’s shirt have anything in common?

1:16 - Notice the geometry of the rug.

1:48 - Think about the geometrical problem that Small Number is solving.

2:25 - A taste of the projective geometry: Are the lines formed by the tiles on the ground parallel or would they meet if they were extended?

2:31 - “I can do a 360° and a 720°.”

2:46 - “Full Angle points to two ramps that are the same height, but different shapes. One is flat, and the other is curved like the inside of a cylinder.”

3:00 - 3:08 - “As the front of his board comes off the ramp, he grabs it and spins around fully two times before letting go and landing perfectly!”

3:20 - “Well, Small Number, then you better be ready to learn some geometry! You will have to learn to do a 360° first.”

Subsection 4.1.5 Answer: How did Full Angle know which ramp to choose in order to have enough time in the air to spin around twice before landing?

This should be treated as an open ended question. The teacher should moderate the discussion to make students aware of the following:

Point 1

The meaning of the phrases ‘360°’ and ‘720°’.

Point 2

To make two rotations (720°) requires more time than to make one rotation (360°).

Point 3

To stay longer in the air, a skateboarder needs to launch themselves very high.

Point 4

The shape of the ramp is related to the height that the skateboarder will reach.

  • Point 1 - Understanding Angles:

    Here is a possible scenario.

    Teacher to the class: “How do you understand the phrases 360° and 720°?”

    \(\color{blue}{Script}\) \(\color{blue}{1:}\)

    Alice (correctly): 360° means that you turn a full circle. 720° means that you turn two full circles.

    Teacher to Alice: “Thank you, Alice!”

    Teacher to the class: “Do you agree with Alice?” [Teacher moderates the follow up discussion accordingly.]

    \(\color{blue}{Script}\) \(\color{blue}{2:}\)

    Alice (incorrectly): 360° means that you turn two full circles. [Or any other incorrect answer.]

    Teacher to Alice: “Thank you, Alice!”

    Teacher to the class: “Do you agree with Alice?” [Teacher moderates the follow up discussion accordingly.]

    \(\color{blue}{Script}\) \(\color{blue}{3:}\)

    No student is replying or the discussion in Script 2 is not converging.

    Teacher to the class: “Why don’t we start with the meaning of 90°, i.e. with the measurement of a right angle?” (Figure 4.1.2)

    Figure 4.1.2. 90°

    Teacher to the class: “What about 180°? Since \(180^o = 2 \times 90^o\text{,}\) this means two right angles which gives us a straight angle.” (Figure 4.1.3)

    Figure 4.1.3. 180°

    Teacher to the class: “Now, what about 360°? Since \(360^o = 2 \times 180^o\text{,}\) this means two straight angles which gives us a full angle.” (Figure 4.1.4)

    Figure 4.1.4. 360°

    Teacher concludes: “So, 360° means that you turn full circle. Consequently, 720° means that you turn two full circles.”

  • Point 2 - Time of Flight:

    Teacher to the class: “Now, I’d like you to stand up and face the window.”

    [After everyone is standing facing the window.] “Think about a line that is perpendicular to the floor and passes through the top of your head.”

    [After waiting for a moment] “Do you know what I mean? Do you have any questions?”

    [Continues after possibly answering students’ questions] “Now, I’d like you to slowly rotate around this imaginary line [that is perpendicular to the floor and passes through the top of your head] for 360°, i.e. turn around till you face the window again. Is this OK? Do you understand what I’d like you to do?”

    [Continues after possibly answering students’ questions] “Also, I’d like to start counting once you start rotating. Remember the number that you reach once you stop rotating.”

    “Are you ready? Go!”

    [After everyone is finished] “Bob, What was the the number that you reached?”

    Bob: [for example] “I counted to 9.”

    Teacher: “Carol, what did you get?” [Teacher makes sure that students associate a number with the rotation.]

    [After a short break] “Now, let us face the window again. This time I’d like you to do 720°, i.e. to stop after two rotations. And, please remember to count the whole time. Try to keep the same speed as when you did 360°.”

    “Are you ready? Go!”

    [After everyone is finished] “Dave, What was the the number that you reached?” Dave [for example]: “I counted to 17.” “Erin, what did you get?” [Teacher makes sure that students associate a number to this activity.]

    Teacher to the class: “Are you surprised that your count for 720° was higher than the count for 360°?”

    Class: “No!”

    Teacher: “Who would like to explain why the second count was higher than the first one?”

    Frank: “Because we needed more time to do 720° than 360°.”

    Teacher: “Excellent thinking, Frank! Thank you!”

    To the class: “Do you agree that Full Angle has to make sure that he stays longer in the air when he does a 720° than when he does a 360°?”

    Class: “Yes!”

  • Point 3 - Air Time:

    For this activity you will need two quarters, two chairs and four volunteers. Place the chairs about 1.5 meters apart facing each other.

    Teacher to the class: “For this experiment, I will need four volunteers.” [Say that Gary, Heidi, Ivan and Judy volunteer to participate.]

    Teacher to the four volunteers: “Gary, please take this coin, climb on the chair, and extend your hand with the coin. Heidi, here is a coin for you. You will sit down on the other chair, and extend your hand with the coin. When I say Go! you will release the coin so that it drops on the ground. Don’t throw the coin, just open your hand and let it go.”

    “Ivan and Judy, your job is to look and listen carefully and to tell the class which coin hits the floor first.” “Do you have any questions?”

    Teacher to the class: “Do you understand what we will do? Do you have any predictions? Which coin will hit the ground first, Grace’s or Heidi’s?” [Class, possibly: “Heidi’s!” “Gary’s!” “Same time!” “Not sure!”]

    Teacher: “Let us check!” [To the four volunteers:] “Are you ready?” “Go!”

    Figure 4.1.7. Coin drop

    Teacher to Ivan and Judy: “What did you observe? Which coin did hit the floor first?”

    Ivan and Judy: “It was Heidi’s coin!”

    Teacher to the class: “Do you agree? Are you surprised with this outcome? Would you like to repeat the experiment?” [Teacher moderates discussion.]

    Teacher to the class: “Who would like to explain why Gary’s coin needed more time than Heidi’s coin to hit the floor?”

    Kelly [correctly]: “Because Gary was standing on the chair, his coin was further away from the floor than Heidi’s coin.”

    Teacher to the class: “Thank you, Kelly! You are absolutely right! Later in your science and math classes you will learn that if an object falls from the height of \(d\) meters then the objects needs about \(\sqrt{\frac{d}{5}}\) seconds to hit the ground.”

    “You will need to know a bit more of physics and mathematics to fully understand what’s going on here. What I would like you to know is that this mathematical expression confirms our observation that the larger height \(d\text{,}\) the longer the falling time \(t\) of the object is.”

    Teacher [concludes]: “So, if Full Angle wants to stay in the air long enough to do a 720°, he must launch himself very high.”

  • Point 4 - Ramp Geometry:

    Teacher to the class: “There are three basic types of the skateboard ramps.”

    Kicker ramp

    The ramp surface is flat.

    Launch Ramp

    The ramp surface is curved

    Quarter Pipe

    The ramp surface looks almost like the inside of a cylinder.

    Figure 4.1.9. Which of these ramps is a quarter pipe?

    Teacher to the class: “One of the reasons that every child in the world who is lucky to go to school studies mathematics, is that mathematics is useful. We are going to use drawings of lines of different shapes to answer Small Number’s question.”

    Teacher continues: “Look at this drawing and imagine that each blue line is a different ramp. Then, the red dotted lines represent the path of the skateboarder. Which of these three ramps in the skateboard park should Full Angle choose”

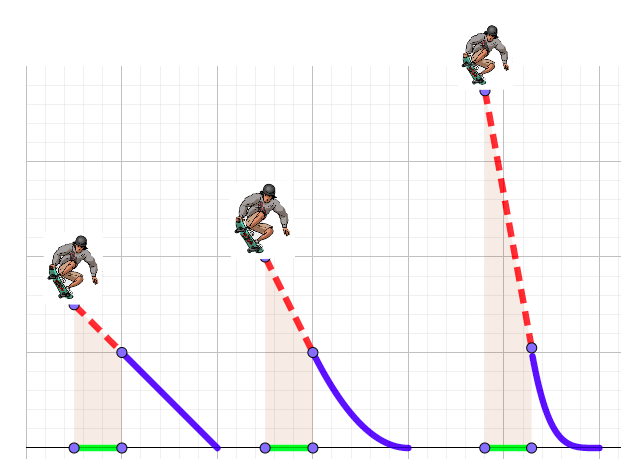
    Figure 4.1.10. Which of these ramps should Full Number choose?

    Class: “Full Angle should choose the quarter pipe ramp because the he would launch himself very high in the air.”

Subsection 4.1.6 Small Number’s Homework Problem

Small Number: Full Angle, can you help me with my homework. This question is so hard that even Perfect Number couldnt solve it.

Full Angle: I can try. What is the question?

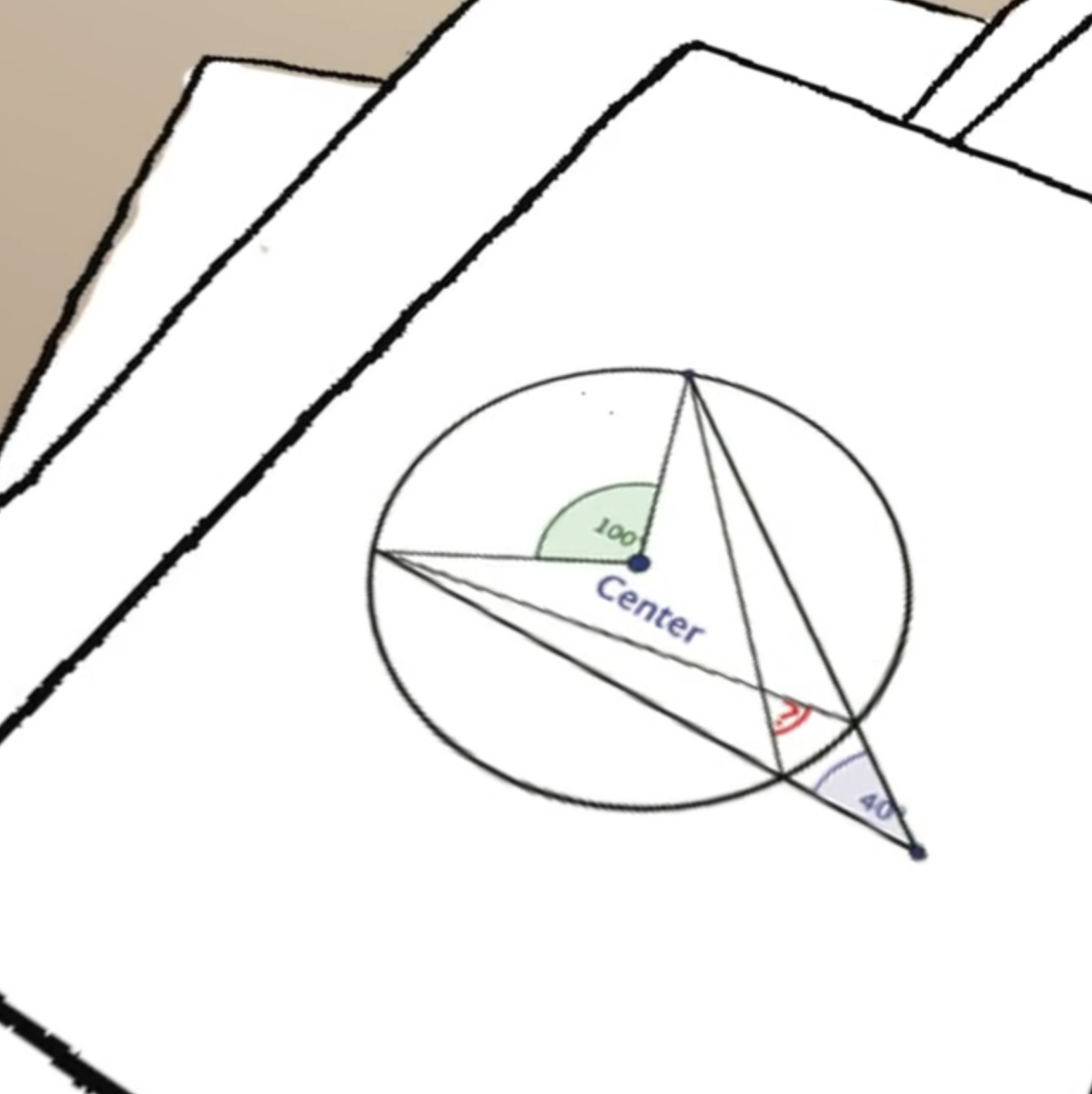
Small Number: I have no idea. This diagram is all I got: (Figure 4.1.11)

Figure 4.1.11. Small Number’s homework problem

I don’t even know where to start.

Full Angle: I agree, it is confusing. Can you tell me what you see in this figure?

Small Number: I see this circle, a bunch of line segments, many points, two angles, and a question mark

Full Angle: (laughing) That’s very good, Small Number.

Full Angle: (seriously) You know, when you have a problem like this, it is always helpful to annotate all of the significant points on your diagram. To avoid confusion, it is a good idea to use capital letters in the alphabetical order. To denote the centre of the circle people often use the capital letter \(O\text{.}\)

Small Number: Like this? (Figure 4.1.12)

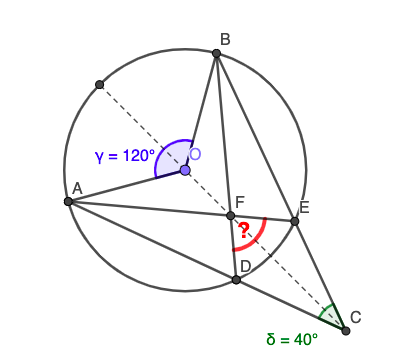
Figure 4.1.12. Small Number uses capital letters to annotate all significant points on the diagram

Full Angle: Excellent work, Small Number! Do you observe any symmetry on your diagram?

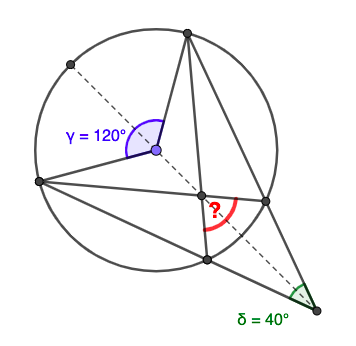
Small Number: Yes, I see that the points \(A\) and \(B\) and the points \(D\) and \(E\) are symmetric to each other with respect to the line through the points \(O\) and \(C\text{.}\)

Full Angle: Very good! Remember that fact, Small Number. You will need it later. Now, can you tell me which angles are given?

Small Number: Oh, I see. I know that \(\angle AOB = 120\)° and \(\angle DCE = 40\)°.

Full Angle: And what do you think that the red question mark stands for?

Small Number: For the [measure of] \(\angle DFE\text{?}\)

Small Number: (scratching his head) I still have no idea how to calculate this number.

Full Angle: (smiling) Patience, Small Number. We are almost there

Full Angle: What if you use your blue felt pen and colour the smaller of the two arcs with the endpoints A and B? Let us see if we can use that arc to calculate the measure of \(\angle ADB\text{.}\)

Small Number: Like this? (Figure 4.1.13)

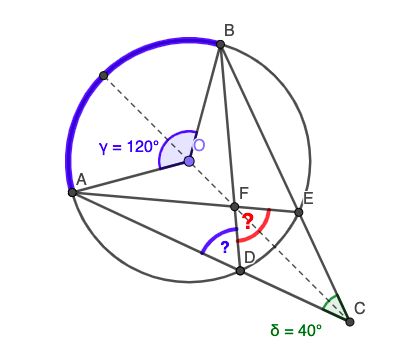
Figure 4.1.13. Small Number colours \(\stackrel \frown {AB}\) and is trying to to calculate the measure of \(\angle ADB\)

Full Angle: Yes, very good. Now, do \(\angle ADB\) and \(\angle AOB\) have something in common?

Small Number: They kind of share \(\stackrel \frown {AB}\) .

Full Angle: Yes, they do! Next, look at the vertices of those two angles, the points \(O\) and \(D\text{.}\) What do you observe?

Small Number: The point \(O\) is the centre of the circle and the point \(D\) is a point on the circle.

Full Angle: Maybe you remember what those angles are called?

Small Number: I think that \(\angle AOB\) is called the central angle, but I don’t remember what we call \(\angle ADB\)

Full Angle: It is called an inscribed angle. Do you remember your teacher talking about the relationship between a central angle and an inscribed angle that share the same arc?

Small Number: I know that \(\angle ADB = 60\)°! It was kind of funny how my teacher got excited when she was telling us that once when you choose the arc then it does not matter which point on the circle you pick as the vertex of the inscribed angle: That angle will be always exactly one-half of the corresponding central angle. So,

\begin{equation*} \angle ADB = \frac{1}{2} \times \angle AOB = \frac{1}{2} \times 120^o = 60^o \end{equation*}

Full Angle: I agree, it is kind of funny that something like that works for all points on the circle!

Full Angle: We need just one more thing and we are done. I’d like you to check if we can somehow connect \(\angle ADB\) and \(\triangle CDF\text{.}\) What if you colour in this triangle?

Small Number: Like this? (Figure 4.1.14)

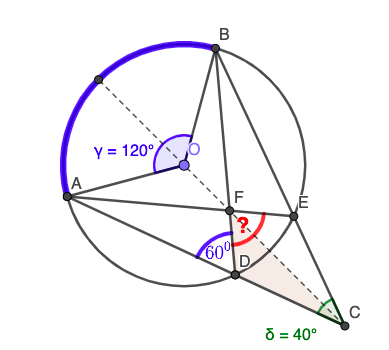
Figure 4.1.14. Small Number writes \(\angle ADB = 600\) and colours \(\triangle CDF\)

Small Number: You should be a teacher, Full Angle! I know what to do next. Because \(\angle ADB\) is an exterior angle for \(\triangle CDF\) it must be:

\begin{equation*} \angle ADB = \angle DCF + \angle DFC \end{equation*}

I know this because of the symmetry:

\begin{equation*} \angle DCF = \angle ECF = \frac{1}{2} \times \angle DCE = \frac{1}{2} \times 40^o = 20^o \end{equation*}

Now it is easy:

\begin{equation*} \angle DFC = \angle ADB − \angle DCF = 60^o − 20^o = 40^o. \end{equation*}

Small Number: (very excited) Mom, I did it! The measure of the unknown angle is 80°!

Small Number’s Mom and Full Angle look at each other, smiling.

Subsection 4.1.7 Challenge

Ask students to make up a problem that is related to circles and triangles and to share their solutions of the problem.

Prove that the measure of any inscribed angle is equal to one-half of the corresponding central angle.