Section 9.1 Small Number and the Four Rabbit Holes - Classroom Guide
View the full story: Small Number and the Four Rabbit Holes
Suggested Grades: 2 – 7
Subsection 9.1.1 Mathematics
- Solving a puzzle - mathematical thinking and understanding of the question and the given conditions
- Strategizing - a sequence of steps that lead to a solution under the given restrictions; following the rules of the game
- Logic - statements of the form “if… then”
Subsection 9.1.2 Mathematical Vocabulary
- small, number, every, early, big, circle, back, edge, four, holes, straight, line, a few, steps, apart, from each other, always, checks, only one, before, entering, one day, many days, one morning, once again, top, every night, the hole that is next to the hole, previous night, keep checking only one hole every morning, in how many days
Subsection 9.1.3 Cultural Components
- Indigenous: Raven and Coyote are common characters in Indigenous storytelling. See Coyote, the Trickster and the Raven and the Oral Tradition of British Columbia’s First Nations
- General: What is a fable? See Wikipedia - Fables. Have you heard about an ancient Greek storyteller named Aesop? He used fables to tell many truths about people. See the Aesop for Children, for example.
Subsection 9.1.4 Mathematical Observations (Video)
Click here to see the film (English)



Opening scene: Notice the shapes of the sun and clouds, the horizon, Coyote’s den, the log, and the four rabbit holes. What is the pattern of trees at the edge of the forrest? Estimate how tall the trees are.
0:13 - Is Coyote’s face symmetric? The shape of Coyote’s ears?
0:16 - What is the shape of Raven’s body and beak?



0:18 - What is the shape of the holes and tree trunk? How many holes?
0:38 - Coyote is checking the second hole from the right.
0:53 - Coyote is checking the second hole from the left.



0:55 - Coyote is checking the most right hole. Raven looks bigger than Coyote - why is this?
1:09 - Now Coyote is looking bigger than Raven - why is this?
1:23 - How would you describe the shape of Raven’s wing?

2:16 - How many circles do you see?
All: How did you like the sound of drumming in the film? Can you repeat the pattern that the drummer was making?
Subsection 9.1.5 Answer: In how many days will Coyote catch the rabbit?
Small Number thinks:


“What if I try to solve this puzzle with three holes only?” (Figure 9.1.1)
“What if the coyote checks the hole on in the middle? What if that hole is empty? That means the rabbit must be in the hole to the right or in the hole to the left.” (Figure 9.1.2.)
“But, the next day the rabbit has to move to the left or to the right! So the coyote should check the middle hole again and the rabbit will be there!” (Figure 9.1.3)

Small Number says:
“Now let me think what the coyote needs to do if there are four rabbit holes.” (Figure 9.1.4)
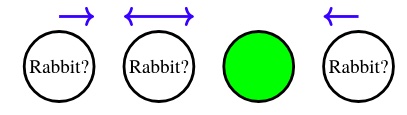
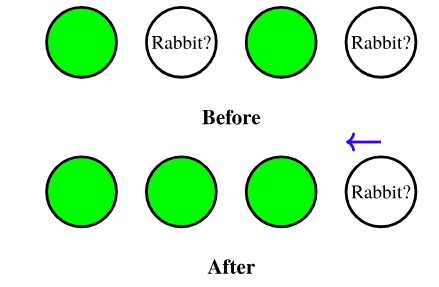
“What if the coyote checks the hole that is second from the right and the rabbit is not there?” (Figure 9.1.5)
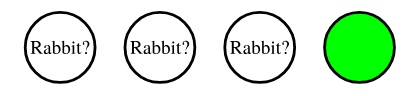
“So the next morning, the coyote will know that the most right hole is empty!” (Figure 9.1.6)
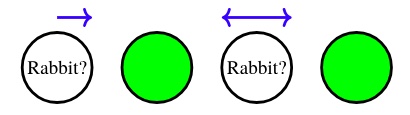
“This looks like the case with three holes! What if the coyote checks the middle hole and the rabbit is not there?” (Figure 9.1.7)
“So when the coyote comes the next morning, he will know that the left most hole is empty and that the second hole from the right is empty.”
“Oh, I see! If he checks the hole that is second from the left and the rabbit is not there, he will definitely catch the rabbit the next day! The coyote will need at most four days to catch the rabbit!” (Figure 9.1.8)
Subsection 9.1.6 Discussion/Activities
Exercise 9.1.9. Grades 2-3.
Students should play the solution out in the class or outside of the class. Start with the case of three holes. Discuss the question with the whole class to make sure that students understand the rules. If possible divide the class in a few groups. In each group ask for volunteers who would be willing to act as the coyote, and the rabbit. Mark three holes on the floor (ground). Ask other students to suggest what the coyote needs to do next. Allow “trial and error” moves and discuss their outcomes.
Exercise 9.1.10. Grades 4-7.
Discuss the question with the whole class to make sure that students understand the rules. Divide the class in pairs and ask each pair to come up with the solution. Encourage students to write down their solutions as a sequence of steps. After 15 minutes invite students to share their solutions. After the first group explains their solution, ask if any other group found a different solution. If yes, invite this group. (The message here is that the same problem can have multiple solutions.) Did the second solution have the same number of steps as the first solution? More solutions? The minimum number of steps? At the end of the class, invite students to think about the case with five or more holes under the same rules. Ask students to bring their solutions to the class and share with their peers.
Exercise 9.1.11. General.
Ask students to pay attention to mathematics (words, geometrical shapes, patterns, numbers). Ask students to pay attention to cultural, particularly Indigenous, aspects of the story. Ask students to share their favourite puzzle with the class.
Subsection 9.1.7 Challenge
How many days would Coyote need to catch the rabbit if there were five rabbit holes? Six? Seven? Ten? A hundred?

