Section 10.1 Small Number and the Abandoned Pit House - Classroom Guide
Authors: Megan Monkman and Kelly Wallace
View the full story: Small Number and the Abandoned Pit House
Subsection 10.1.1 Mathematics
- estimation and approximation
- right triangles: pythagorean theorem, pythagorean triples, 3:4:5 ratio
- geometry: shapes, patterns
- circles: diameter, radius

Subsection 10.1.2 Mathematical Vocabulary
Small, number, young, a lot, near, ever, many, often, group, every, only, few, all, one day, big, circle, everything, once, across, over, quicker, middle, empty, through, hole, lying on, around, faster, wide-open, beam, vertical, dome, above, inside, enclosed space, short, edge, ends, long, part of, circular, ring, hundreds, huge, right away, soon, closer, into, run towards, tightly, at least, three, eight meters across, twice as large, everyone, five meters long, how many, back to, perpendicular
Subsection 10.1.3 Cultural Components
Note: This story was inspired by the pithouse construction display at the Secwépemc Museum and Heritage Park in Kamloops, British Columbia.
-
Indigenous:
- What is a pithouse? See: Canadian Encyclopedia - Pithouse, No Place Like a Pithome, Pre-contact pithouses, Pithouses across many cultures.
- What is a traditional territory? Which traditional territories do we reside on? Which Nations do these territories belong to? See: Interactive BC Map.
- What does mother tongue mean? Do you know any other languages? What languages do the Nations we learned about speak? See: First Voices.
- Who are your ancestors? Can we list our ancestors? How many do you know of? How many do you think there are? Definition of ancestors, Do the math - how many ancestors do I have?, Indigenous ancestry and identity.
- Check out this student built pithouse at UNBC: UNBC pithouse (video).
- Pythagorean Extension: First peoples constellations. See: BC Curriculum Math 8, Indigenous constellation names.
- Extension Question: How was the pithouse ventilated, how was it safe with a fire? Read more about how a ground surface air hole, and a hole in the roof would have allowed ventilation and for smoke to escape.
-
General:
- Does your family have any cultural traditions or rituals? What are they? See: Traditions from around the world.
- Do your family members tell you stories? What stories do they tell? Have you ever listened to stories from your grandparents?
- Do you speak any other languages?
- Have you ever been in a situation that felt completely new? Have you ever been lost after finding new surroundings? How did you explore your new surroundings? Were you prepared?
- More about mathematics and architecture: Mathematics and Architecture.
Subsection 10.1.4 Mathematical Observations (Video)
Click here to see the film (English)



Opening Scene: Notice the geometry of the pit house roof. What shapes can you see? Do you notice different sets of parallel lines? Can you estimate the angles that are seen in this structure?
0:13 - Notice the shape of the fence. How many fence pieces can you see?
0:47 - 0:54 - “Even though Small Number only understands a few words, he enjoys listening to his grandpa when he speaks in the language of their people.” How many words do you know of another language? Is that a few? Or a lot?



1:17 - How many buttons can you see on Grandpa's shirt? Do you think there are more buttons that we can't see?
1:37 - Can you estimate the height of the fence? Or the size of the fenced area? What clues can you use to help you make a closer guess?
1:49 - What shapes can you see? How deep do you think Small Number might have fallen through the grass?



1:59 - “He could feel his heart beating faster.” Can you measure how many times your heart beats in one minute? How does it change after running up a flight of stairs?
2:08 - What do you notice about the beam of light? What shape is the light beam most similar to? What shape does a beam of light show when it points towards a flat surface?
2:24 - What types of angles can you identify in the logs? (acute, obtuse, right, straight, reflex)



2:26 - 2:34 - “He could see that the short poles at the edge of the floor and the ends of the long poles were part of the roof that formed a circular ring-like shape.”
2:36 - “There must be hundreds of poles used to build this room.” How many wooden poles can you count? How many of the poles are thick? How many are thin?
3:13 - What shape is the opening that Grandpa comes through? Can you estimate how wide and tall the opening is?



3:33 - “The hole must be about 3 metres above the floor.”
3:48 - “This is not a very big house, maybe it is only 8 meters across. The Chief's pit house could be twice as large.”
4:12 - “So, those posts are about five meters long.”

4:23 - “I wonder how our ancestors knew how many posts they needed to build the roof?”
Subsection 10.1.5 Answer: Why did Small Number think that the posts used to build the roof were about five meters long each?
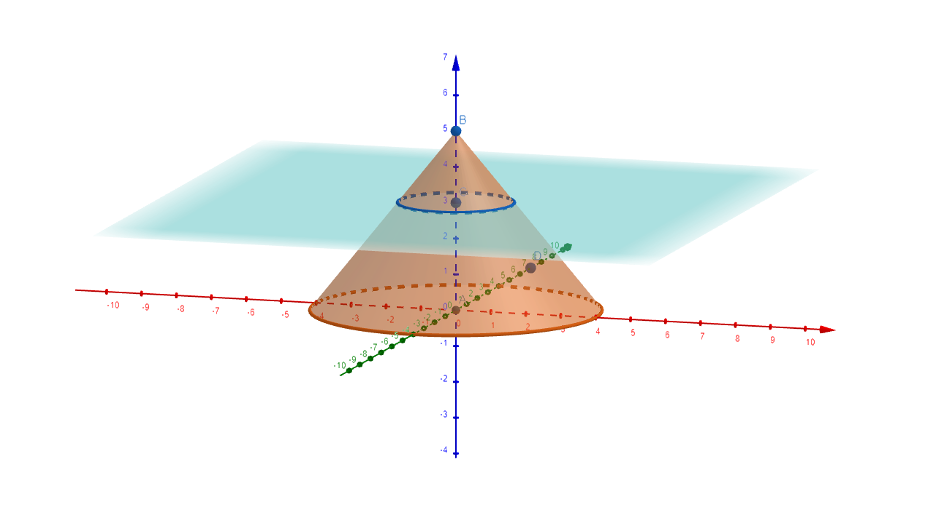
Small Number finds himself at the bottom of the abandoned pithouse. Examining his new surroundings, he notices the long and short poles that construct the room. They form part of a circular dome-like roof.
Small Number thinks, “there must be hundreds of poles used to build this room”.
Small Number is lost and scared, so he calls Grandpa for help.
Small Number's grandpa arrives and shares with him that, “this is not a very big house, maybe it is only eight meters across”.
Small Number remembers that the shape of the pithouse was circular and thinks to himself, “the radius of a circle is half of its length across”.
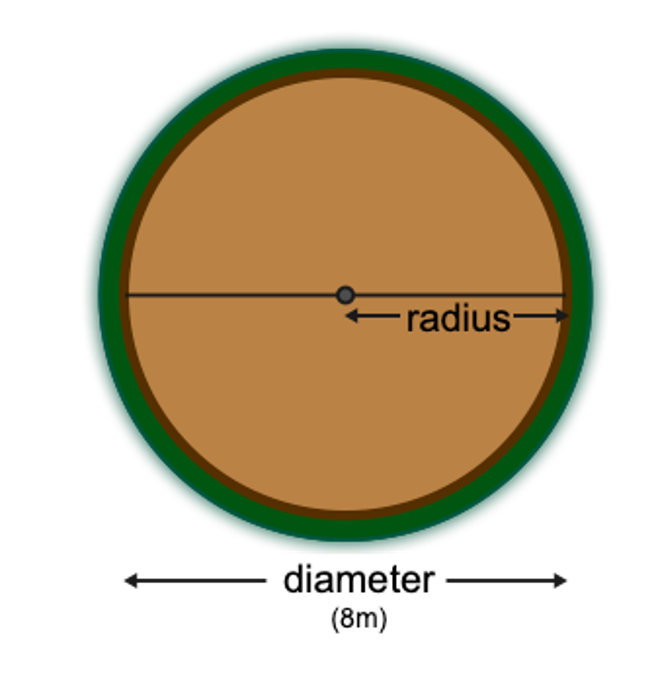
Small Number deduces, “the diameter of the pithouse is eight meters, so the radius must be four meters”!
Grandpa also shares that he estimates the hole to be at least three meters above the floor. Small Number recognizes that the height of the pithouse is perpendicular to the floor, which means that they intersect at 90 degrees.
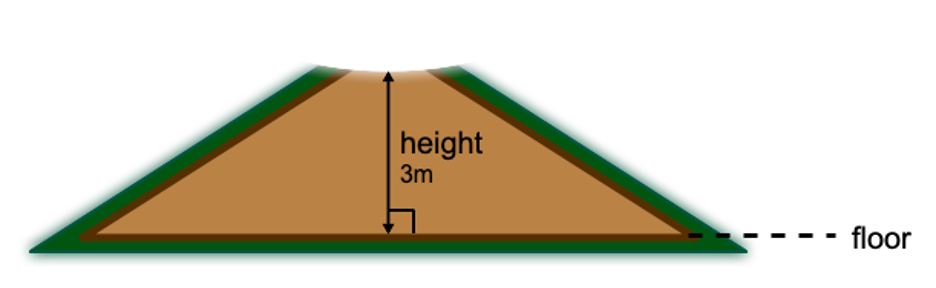
Small Number then thinks back to the hundreds of poles used to construct the pithouse. He notices that a triangle is formed by the height of the pithouse, half of the length of the floor, and the poles. Since two of the sides of this triangle meet at 90 degrees, Small Number recognizes it as a right triangle!
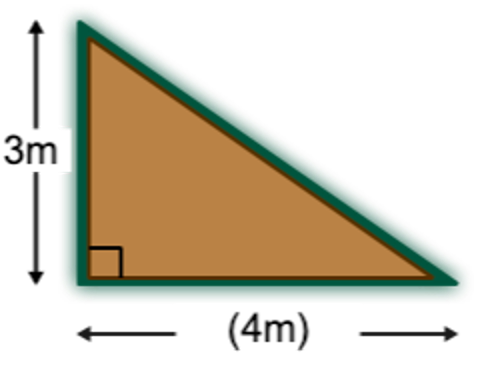
Small Number gets excited! He knows that right triangles have special properties! Small Number begins to get curious… maybe he can use these special properties to determine the length of the poles used to construct the roof.
Becoming even more excited, he remembers back to his most recent math lesson at school. The class learned about Pythagorean triples - sets of 3 positive integers that form the side lengths of a right triangle. However, Small Number can't remember the missing side length for a triangle with other side lengths of 3 and 4.
Luckily, Small Number does remember learning about the Pythagorean Theorem! Small Number knows he can use the Pythagorean Theorem (\(a^2+ b^2 = c^2\) ) to determine the missing side of the right triangle - and this would be the same length of the poles used in the roof!
Small Number notes to himself, “\(c\) represents the length of the hypotenuse of a right triangle, and \(a\) and \(b\) represent the other sides”.
Small Number decides that since the other side lengths of this right triangle are approximately 3 and 4 meters long, he can set up the Pythagorean Theorem as follows:
Therefore, the length of the poles has to be close to 5 meters! This also means that the Pythagorean triple Small Number thought about must have had the 3:4:5 ratio! Now he remembers!
“So, those posts are about five meters long” says Small Number, pointing to the roof. “I wonder how our ancestors knew how many posts they needed to build the roof?”
Small number decides to save that question for another day…
Subsection 10.1.6 Discussion/Activities
Exercise 10.1.1. Level 1 (grades 4-5): Identifying Triangles and Circle Vocabulary.
-
Start with the following questions:
-
What is a triangle? Can someone draw one on the board?
Definition: A triangle has 3 angles and 3 sides.
Where can we find triangles in the classroom?
Where can we find triangles outside of the classroom?
-
What is a circle? Can someone draw one on the board?
Definition: A circle is a set of points equidistant from one particular point, the centre.
What are the properties of a circle?
Is an oval a circle? Why or why not?
- Where can we find circles in the classroom?
- Where can we find circles outside of the classroom? In nature?
-
Check out the Coast Salish Design elements here. Can you identify any triangle-like shapes? Compare the similarities and differences between triangles and trigons. Can you identify and measure the different components in any circles or ovals?
-
Suggestion: A gym activity
Challenge the students to find circles and triangles within the gym.
If you have access to a circular parachute, use this to demonstrate radius and diameter. You can measure across using the student's arm lengths.
Source: https://iteachmorethangym.wordpress.com/2017/12/12/does-your-gym-floor-help-you-teach/
-
Suggestion: Create circles and triangles ahead of time and distribute them to the class. Do so with a variety of sizes and types. Consider incorporating traditional Indigenous artwork into this task, such as this.
Challenge students to identify parts of a circle (radius, diameter, circumference) using rulers. Use string to measure the circumference.
Challenge students to identify parts of a triangle (hypotenuse, side lengths, angles, base, height) and measure using rulers and protractors.
Challenge students to identify different types of triangles (right triangles, isosceles triangles, etc.), confirm their identity by measuring.
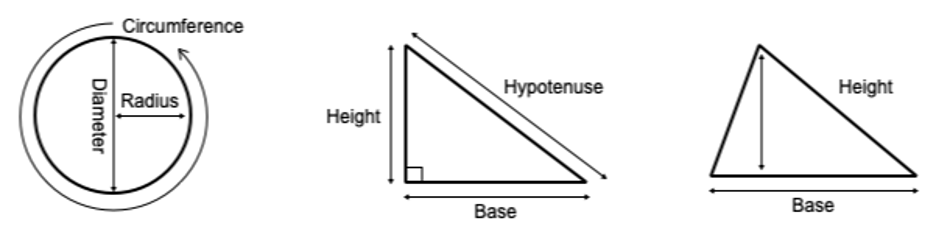
Exercise 10.1.2. Level 2 (grades 6-8): Pythagorean Triples and Pythagorean Theorem.
-
Start by asking the following questions:
What is a right triangle?
What characteristics do right triangles have? (90 degree interior angle, hypotenuse: longest side of the triangle is across from the 90 degree angle, height, base, angles add up to 180 degrees)
Compare right triangles to other types of triangles; what types do we know? (isosceles, scalene) Can these also be right triangles?
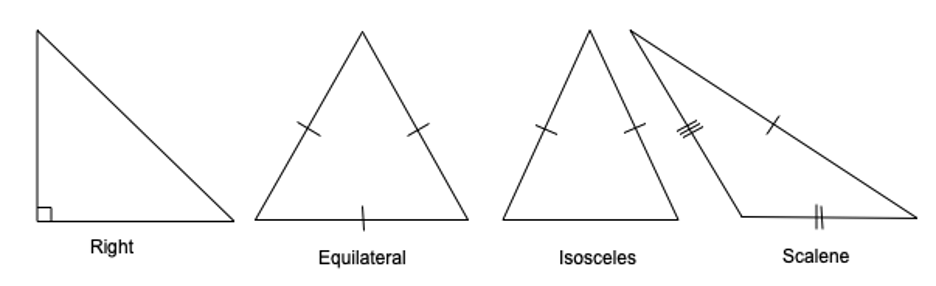
-
Define Pythagorean Triple: A right triangle such that all three side lengths are positive integers (natural numbers).
Mention the example of a Pythagorean triple (3:4:5) and ask, what if we had a triangle with sides (6:8:__)?
Question: How many pythagorean triples are there?
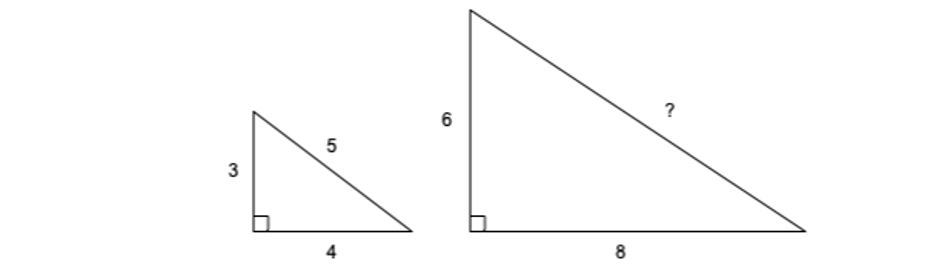
-
Introduce the pythagorean theorem in the context of the (6:8:__) triangle (use the Pythagorean theorem to determine the missing side length). Note that the square of the hypotenuse is the sum of the squares of the base and height.
\begin{equation*} \text{hypotenuse}^2 = \text{base}^2 + \text{height}^2 \end{equation*} -
Activity:
This activity will take 2 students. Have them start at the same point and have one student walk forward 4 steps and then walk to their right by 3 steps. Ask them to estimate how many steps it will take to return to their original spot directly. Ask them if it is more than 3 or 4? (It should be about 5)
-
Activity:
This activity will require grid paper (printed on white and coloured paper), scissors, and gluesticks.
On the white grid paper, draw a line segment 3 units in length near the centre of the paper.
At a right angle from the first line segment, draw a second line segment 4 units in length.
Complete the triangle by drawing a line connecting the two open ends.
Using coloured grid paper, cut out squares with sides lengths that are the same length as each side of the triangle (3x3, 4x4, and students will find that the square for the hypotenuse is 5x5)
Lay each square along its corresponding side of the triangle and tape it into position.
Using the white grid paper, cut out one more of each of the two smaller squares.
Cut or manipulate these smaller squares so that they fit on the larger square.
IDENTIFY the relationship that exists among the areas of three squares. (the sum of the area of the two smaller squares is equal to the area of the large square).
-
Pythagorean Theorem Video:
This video shows the physical relationship between the variables in the Pythagorean theorem in an engaging demonstration using a water apparatus.
-
Square Number Wikipedia:
This wikipedia page beautifully illustrates the patterns found in square numbers. This also demonstrates why we call them Perfect Squares.
Subsection 10.1.7 Challenge
Coast Salish Longhouses (Pythagorean theorem):
Coast Salish Longhouses are built with either a shed or gable roof (as in the figure below). Traditional materials, such as cedar, are used to construct the plank siding, and post and beam structure. Longhouses, as you may guess, are typically long and narrow. Most often, traditional longhouses had interior ornamentation - crest and totem carvings were located inside rather than exteriorly.
Source: https://www.vancouverheritagefoundation.org/house-styles/traditional-coast-salish-plank-houses/
Use the Pythagorean theorem to determine the length of the roof to be covered by cedar planks:
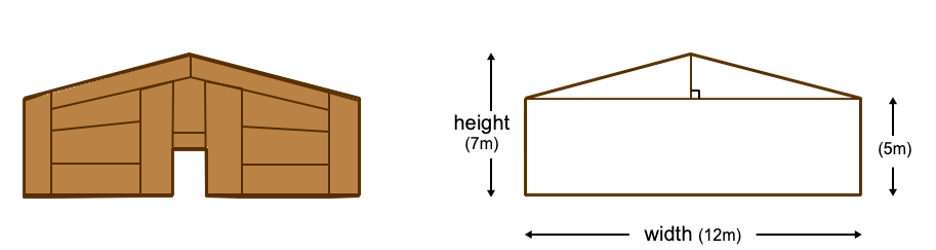
Is the triangle (made up by the roof) a pythagorean triple? Why or why not?
Pithouse Roof (Circle Geometry / Problem Solving):
Small Number asked Grandpa, “I wonder how our ancestors knew how many posts they needed to build the roof?”
The area of a circle can be determined using the following formula: \(A = \pi r^2\) and the surface area of a right circular cone is \(A = \pi r(r + \sqrt{h^2 + r^2}) \text{.}\)
Is this enough information for Small Number to estimate the number of posts needed to build the circular roof covering the pithouse? What other information might we need?
How can we use these area formulas to help Small Number?
Pithouse Volume (Problem Solving):
How could we estimate the volume of the pithouse? Remember, the volume of a right circular cone is \(V = \pi r^3 \frac{h}{3}\) where \(r\) is the radius of the base, and \(h\) is the height. What other information might we need to calculate the volume?
Here is a cone with radius 4. You can see the intersection with the plane (in green), what does this intersection represent for our pithouse?