Adventures of Small Number: Classroom Resources

Subsection 6.1.1 Mathematics

1. Introduction of the number \(\pi\)
2. Collecting data
3. Estimating

Subsection 6.1.2 Mathematical Vocabulary

• small, number, a lot, perfect number, patterns, smooth surface, puzzled, many, different, before, enough, entered, behind, big, starts, over, large, group, close, up, straight, at least, 50 meters, tall, down, widen, fastens, full of, must be, thousands, quickly, back, behind, after, a few, moments, all, out, the other, huge, three, under, the most, all the time, behind, turns around, very much, again, the biggest, so big, at least eight, around

Subsection 6.1.3 Cultural Components

1. Indigenous:

   1. Traditional basket weaving. See, for example, Coast Salish Baskets and Coast Salish Weaving Tools and Technologies.
   2. The role of cedar trees in the traditions of Pacific Coast First Nations. See Cedar.
   3. The role of salmon in the traditions of Pacific Coast First Nations. See Tribal Salmon Culture, Return to the Water: First Nations Relations with Salmon
   4. Did you notice the First Nations art in Grandma’s house?
   5. At which time of the year does Grandma go to the forest to harvest the cedar roots?
2. General:
   1. Have you ever walked through a forest? If yes, did you “smell the sweet scent of the forest”? Did you hear “how the birds sing to each other somewhere high in the trees”?
   2. Did you know that bears eat salmon? Do you know why salmon are so important for the ecosystem? See for example Why Protect Salmon.
   3. Have you ever used what you learned in your math class to estimate some quantities or distances?
   4. Do you hug your grandparents when you see them?
   5. Have you heard about the number \(\pi\) before? There are many resources where one can learn about the history of the number. See for example A Brief History of Pi and The History of Pi. Are you surprised that over many centuries different cultures all around the world have been using the number \(\pi\text{?}\)

Subsection 6.1.4 Mathematical Observations (Video)

Click here to see the film (English)

Subsection 6.1.5 Answer: How wide was the Bear Tree?

Small Number thought:

“The trunk of the tree was so big that I would need at least eight of my friends to hold their hands to get around it.”

Small Number thought a bit longer and then he said:

“Perfect Number, please help me! I’ll stand up and spread my arms. You take Grandma’s sewing measuring tape and measure my arm span”.

A few minutes later, Perfect Number had measured Small Number’s arm span: “Exactly 140 cm!”.

“Funny, that is exactly how tall I am” said Small Number. “So the circumference of the trunk is about 8 \(\times\) 140 centimetres.”

“Let me think: 8 \(\times\) 100 = 800 centimetres. That is 8 meters. And 8 \(\times\) 40 = 320 centimetres. That is just a bit more than 3 meters. So, the circumference of the trunk of the Big Tree is just a bit more than 8 + 3 = 11 meters!”

“But how do I calculate how wide the Bear Tree was?”

Perfect Number smiled: “Have you ever heard about the number \(\pi\text{?}\)”

Small Number was puzzled: “Did you say the ‘number pie’?”

“Let me show you something, Small Number. Let us take three of Grandma’s plates that are the shape of a circle: a big plate, a medium plate, and a small plate. Let us measure their circumferences and their diameters. Then you will use your calculator to divide each circumference by the diameter. You will see, something very cool will happen!”

Small Number and Perfect Number measured three circumferences and three diameters and Small Number used his calculator to divide each circumference by the corresponding diameter. This is what they found:

Small Number shook his head: “Did I make a mistake? Was the first number also supposed to be 3.2?”

Perfect Number was laughing: “This is why I like mathematics! Sometimes you can be both right and wrong”.

She continued: “You were right when you said that we made a mistake! But we didn’t make a mistake in our calculations. You know, Grandma’s sewing measuring tape is not the best tool to measure the circumference! So what we got were just estimates of the lengths that we measured. I know that Grandma would do a better job than we did, but even her measures would be estimates, probably more precise than ours”.

“You are right, Small Number, those three numbers should be equal to each other. But, because our measures were just estimates, all three quotients were also just estimates, so none of those three numbers 3.1607, 3.2 or 3.2 were exactly what we were looking for.”

“If we had a super-precise device to measure the circumference and the diameter then the quotient in each case would be something like 3.14.”

Perfect Number was very excited: “Isn’t that amazingly cool: It does not matter how big your circle is, when you divide its circumference by its diameter you always get the same number! We call that number \(\pi\)”.

“Wow”, said Small Number. “So the number \(\pi\) is equal to 3.14?”

Perfect Number smiled: “No, 3.14 is just an estimate of the number \(\pi\) that everyone knows. For example, 3.14159 is a better estimate of \(\pi\text{.}\) You will learn in high school that those digits go on forever. Another estimate of the number \(\pi\) that many people use is the fraction \(\frac{22}{7}\text{.}\)”

“But, can you tell me now how wide the Bear Tree was?”

Small Number was thinking aloud: “So the width of the Bear Tree is the same as the diameter of the circle with the circumference that I estimated to be 11 meters. If I divide the circumference by the diameter I get the number \(\pi\text{.}\) But this means that if I multiply the width and the number \(\pi\) I get the circumference. So, if I divide the circumference by \(\pi\text{,}\) I will get the width!”

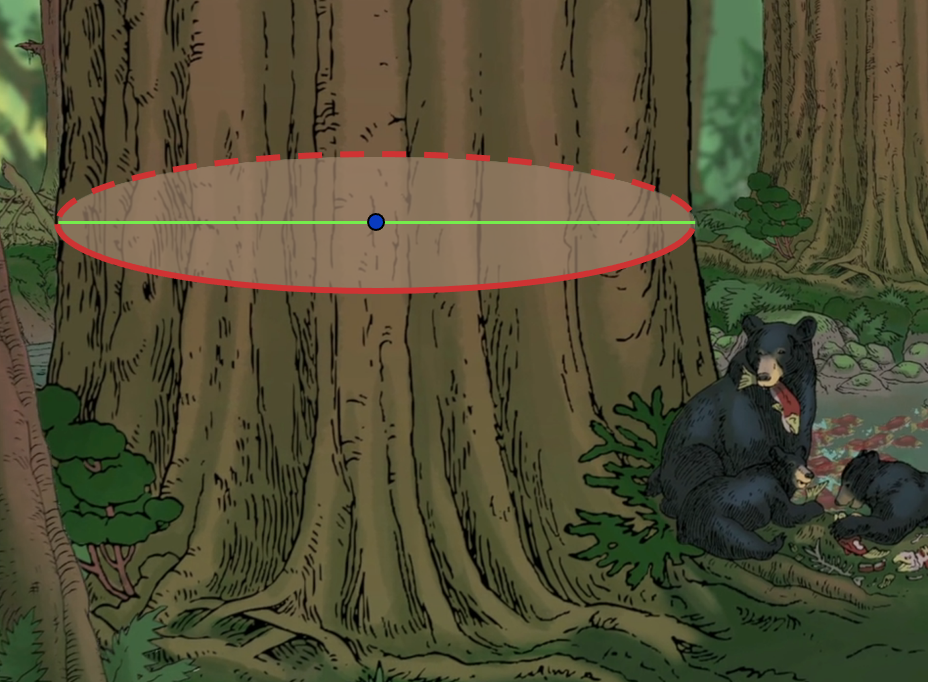
Small Number reached out for his calculator and typed in 11 \(\div\) 3.14, hit enter and yelled: “The Bear Tree is about 3.5 meters wide!”

Subsection 6.1.6 Discussion/Activities

Subsection 6.1.7 Challenge

Memorize a hundred digits of \(\pi\text{.}\) (Reference: a Hundred Digits of \(\pi\))