Adventures of Small Number: Classroom Resources

Point 1 - High Tide Versus Low Tide:

Here is a possible scenario:

Teacher to the class: “How do you understand the phrases ‘high tide’ and ‘low tide’?”

\(\color{blue}{Script}\) \(\color{blue}{1:}\)

Alice (correctly): “Low tide is when the ocean is far from the shore. My grandma also says that ‘the tide is out’.”

“High tide is when the ocean is close to the shore. My grandma also says that ‘the tide is in’.”

Teacher to Alice: “Thank you, Alice!” And then to the class: “Do you agree with Alice?” [Teacher moderates the follow up discussion accordingly.]

\(\color{blue}{Script}\) \(\color{blue}{2:}\)

Alice (somewhat vague): I've heard my grandma saying ‘the tide is out’ and ‘the tide is in’. I think that when ‘the tide is out’ then the ocean is close to the shore.

Teacher to Alice: “Thank you, Alice!” And then to the class: “Do you agree with Alice?” [Teacher moderates the follow up discussion accordingly.]

\(\color{blue}{Script}\) \(\color{blue}{3:}\)

No student is replying or the discussion in script 2 is not converging.

Teacher to the class: “Why don't we start with these two beautiful drawings by Bethani?”

“Look at the two images carefully. What is common between both images? What is different?” (Figure 5.1.2)

[Teacher moderates the discussion. Possible answers: common - the beach, the ocean, the tree, the children, the sand castle; different - the sea level, the sand castle is in the water, the children are much closer to the tree.]

Teacher to the class: “A long long time ago, people noticed that the ocean level was continuously changing. For example, if you look at Bethani's drawings, the tree is always at the same place. But, on one drawing the ocean seems far away from the tree and on the other it is much closer to tree. In the first case we say that ‘the tide is low’ or that ‘the tide is out’. In the other case we say that ‘the tide is high’ or that ‘the tide is in’”.

Teacher to the class: “I wonder if any of you have noticed if the tide was low or if it was high when you went to the beach last time. In any case, pay attention when you are near the ocean next time. Think if you can tell if tide is rising or falling. One useful trick for identifying whether the tide is coming in or out is observing how much seaweed is present on the water line. During a rising tide, more seaweed is pushed onto the beach”.

Point 2 - the Engineering of a Fishing Net:

Teacher to the class: “Here is an image of the net that Small Number and his dad were preparing.” (Figure 5.1.4)

Teacher to the class: [After making sure that each student has a chance to see the image] “Observe different parts of the net: the net itself, the rope on the top of the net, the rope at the bottom, and the attached rocks and the pieces of cedar” [After waiting for a moment:] “Who would like to describe the net and the purpose of each of its parts?”

[A few hands go up. The teacher chooses Bob, for example.]

Bob: “I think that Small Number said something like: ‘This anchor will hold the net in place, the pebbles will keep one edge of the net on the bottom and the pieces of cedar will float and keep the other edge of the net on the surface.’”

Teacher: “Thank you, Bob. Do you know that the rope at the bottom of the net is called the footrope or leadline? The top edge of the net is attached to a rope called the headline or floatline.” [To the class:] “What would happen to the net if Small Number's dad didn't put the rocks on one side and the pieces of cedar on the other side?”

[Teacher moderates the discussion with the goal that students realize the purpose of the objects attached to the net: without the rocks, the net would just float on the surface; with the rocks but without the pieces of cedar (floats) the net would sink. The teacher should lead students to conclude that there must be a balance between the weight of the rocks and the number and the size of the floats.]

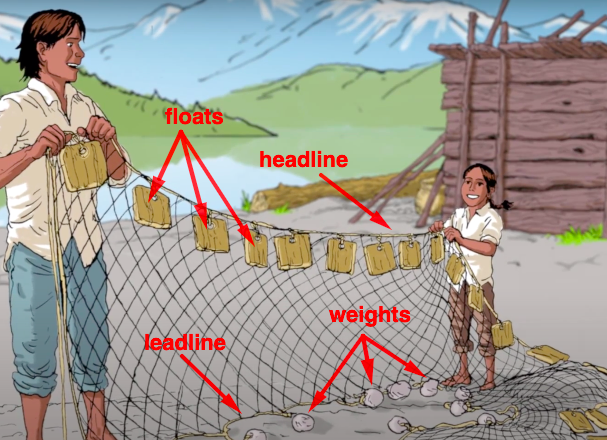
Teacher: “Do you think that the pattern of the net matters? Are the size of the gaps in the net important? Is it possible for the gaps to be too small or too big?”

[Teacher moderates the discussion with the goal of making students aware that the net is designed so that every part has a purpose. The teacher should look for an opportunity to introduce engineering as “the application of science to the optimum conversion of the resources of nature to the uses of humankind”, as it is stated in Encyclopedia Britannica.]

Point 3 - the Area of a Rectangle:

Teacher draws a rectangle on the board and writes:

See Figure 5.1.7.

Teacher: “Do you remember how we can obtain this formula?”

[Teacher moderates the discussion. If needed, the teacher may draw a grid inside of the rectangle and ask “How many squares do we need to cover the rectangle?” See Figure 5.1.8.]

Teacher: “What will happen to the area of the rectangle if we keep the length of the rectangle the same but we shrink the width?”

“What do you think will happen if we shrink both the length and the width?”

Carol: “I think that in both cases the area will also shrink.”

Teacher: “Very good, Carol! Can you explain why the area would be smaller if we keep the length the same but shrink the width?”

Carol: “I think that if we keep the length the same and we make the width smaller then there will be less squares in the grid inside of the rectangle. So, the area will be smaller than it was initially. For example, the area of the rectangle with a length of \(5\) and a width of \(3\) equals to \(5 \times 3 = 15\text{.}\) If we keep the same length but make the width only \(2\text{,}\) then the area of this new rectangle equals to \(5 \times 2 = 10\) which is less than \(15\text{.}\)”

Teacher: “Excellent thinking, Carol!” [To the class:] “Do you agree with Carol? Do you have any questions for Carol?”

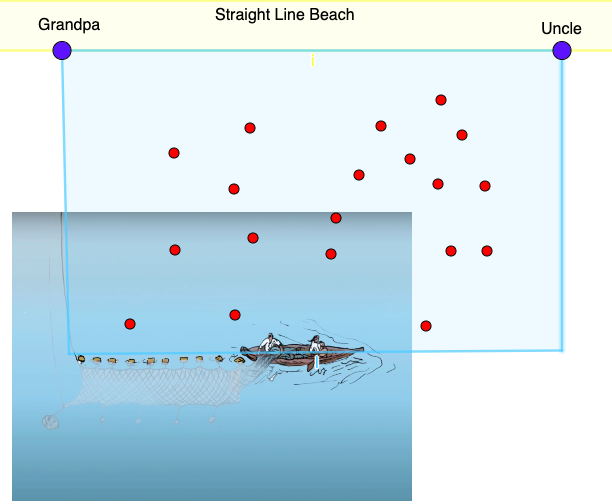
Teacher: “Now let us go back to the story. Do you remember how Small Number and his dad stayed in the canoe and how they were putting out the net? What they actually did was to create a rectangle. In this rectangle one side was the net, and another side was the segment of the beach between Grandpa and Uncle. The other two perpendicular sides were the lines of the net.” (See Figure 5.1.9.)

[Teacher gives the students a moment to analyze the image in Figure 5 and answers possible questions like, “What do the red dots represent?” A: “Each dot represents one salmon.” Maybe this is an opportunity to remind students that in mathematics we use symbols, like letters, numbers, and geometrical figures to represent various objects or entities.]

Teacher to the class: “What will happen when Grandpa and Uncle, with help of Dad and Small Number, start pulling the lines?” See Figure 5.1.10.

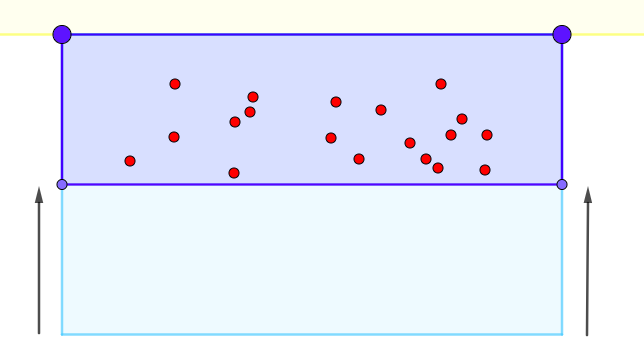
[Teacher moderates the discussion with the goal that students observe how the length of the rectangle stays the same, but the width of the rectangle shrinks. This should lead to the conclusion that the area between the net and the beach gets smaller. Students should also observe that the number of salmon trapped by the net (i.e., the number of salmon contained in the new rectangle) is the same as before.]

Teacher to the class: “What will happen when Grandpa and Uncle start walking towards each other?” See Figure 5.1.11.

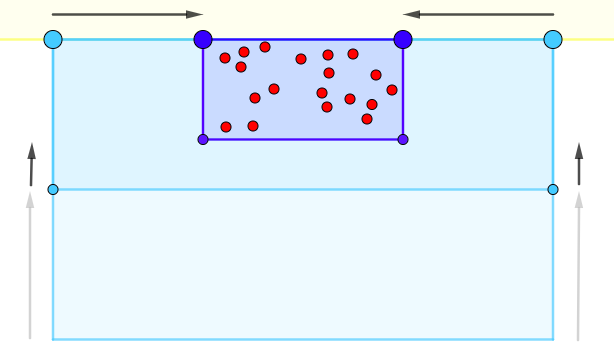
[Teacher moderates the discussion with the goal that students observe how the length of the rectangle gets smaller. This should lead to the conclusion that the area between the net and the beach gets smaller. Students should also observe that the number of salmon trapped by the net (i.e., the number of salmon contained in the new rectangle) is the same as before.]

Hopefully, someone will observe that in this case the net will not stay parallel to the beach. Teacher should seize this opportunity to praise the student and follow up with questions like: “What do you think that the shape of the net will be?” A: “Possibly something like the letter ‘U’.” Also,“Do you think that the area between the net and the beach will get smaller?” or “Will the number of salmon trapped by the net stay the same?”

Point 4 - Exploring Density:

Teacher to the class: “Have you heard of the word dense or the word density? If yes, who would like to explain the meaning of these words?”

Dave: “My mom says that my hair is dense.”

Teacher to Dave: “Yes, I agree with your mom. Your hair is dense.”

Teacher to the class: “Do you think that your hair is dense? What does that mean anyway? How would you understand if I say that a forest is dense?”

[Teacher moderates the discussion leading students to the conclusion that something dense contains a lot of things in a small area.]

Teacher to the class: “I'd like you to look at the three images in Figure 5.1.13. Each of these rectangles contain exactly 20 salmon (represented by red dots).”

A

B

C

Teacher: “Would you say that the group of salmon in the left most image is dense?” [Class: “No!” or “Not really!”]

Teacher: “What about the salmon in the image in the middle? Is it dense?” [Class: “Not really!” or “More than in the first image.”]

Teacher: “What about the group of salmon in the right most image?” [Class: “Yes!” or “More than in the first and second images.”]

Teacher: “I would like you to think about the following: Each image contains the same number of salmon. We agreed that the group of salmon in the left most image was not dense and that the group of salmon in the right most image was dense. So, how come the same number of salmon is dense in one case and not dense in the other case?”

Erin: “I know! The area of the rectangle has shrunk, so the salmon get much closer to each other!”

Teacher: “Excellent thinking, Erin!”

To the class: “Do you agree with Erin? Do you have any questions for Erin?”

[Teacher moderates the discussion with the goal of making students aware that whether something is dense or not really depends on two things: (1) the number of items, and (2) the area that contains those items.]

Teacher: “Mathematicians like to use numbers to compare different items of the same kind.”

Teacher: “For example, if I ask you, ‘How many siblings do you have?’ you will each give me a number and then I can tell who has the most siblings in our class.”

Teacher: “The same is true with the question of if something is dense or not. So, what do you think, how can we get a number that would tell us something is more dense than something else?”

[Teacher moderates discussion. If needed teacher reminds students that at the beginning we have two numbers: (1) the number of salmon, and (2) the area that contains those items.]

An example may be helpful. Recall that each of the three images in Figure 8 have 20 salmon. Say that the area of the left most rectangle equals to 200 square meters, the area of the rectangle in the middle equals to 100 square meters and the area of the right most rectangle equals to 40 square meters.

Teacher: “Should we add or subtract these two numbers?” [A: No! We cannot add apples (the number of salmon) and oranges (the area of the rectangle).] “Maybe we should multiply or divide? Let us see what makes the most sense.”

Consider the following table:

Recall that we observed the same number of salmon got more dense when the area got smaller. Now compare the numbers in the columns “\(20\times \text{Area}\)” and “\(20\div \text{Area}\)”. In which of these columns do you notice this pattern?

A: The column “\(20\div \text{Area}\)”. [Observe that in the column “\(20\times \text{Area}\)” a larger area produces a larger outcome.]

Teacher: “The number that we obtain when we divide the number of salmon by the area is called the density of salmon (per unit of area).”

Point 5 - the Best Tide to Fish in:

Teacher: “Let me remind you about the question at the end of the film: Why did Small Number think that during a low tide the catch would be much smaller?”

Teacher: “So, what do you think? Does it make sense to you that during a low tide the catch would be much smaller?”

Frank: “I think salmon come in with the tide.”

Grace: “I agree with Frank, the incoming tide can push salmon inshore. So, during the high tide there will be more fish close to the shore.”

Teacher: “Thanks, Frank and Grace. You are both correct. An incoming tide is pushing more water towards the beach. This is one of the reasons that the currents that go with the incoming tides are called flood currents. With water, the incoming tide pushes all kind of fish towards the shore.”

“But, often things are not as simple as they may appear.”

“Every fishing location is different. Many fishers think that the only way to develop a pattern about when fish are most likely to show up is to fish there often and record the findings.”

“First Nations have built their knowledge about harvesting salmon and the patterns of tides over a long period of time. This knowledge is part of what we call Traditional Knowledge.”

“I think that Small Number's grandpa, dad, and uncle knew everything that was there to know about the pattern of tides at Straight Line Beach. Do you agree with me?” [Class: “Yes, we do.”]

“Maybe it will surprise you to hear that during the high tide salmon and other fish get closer to the beach in search of food.”

“Did you know that a salmon's diet includes fish? I've read an article in which the author said that during the incoming tide, salmon position themselves close to the shore, turn towards the ocean, open their mouth, and just wait for the tide to push small fish into their mouths.”

Teacher: “So, do you think that Small Number was right when he said that during a low tide the catch would be much smaller?” [Class: “Yes, we do!”]

Point 6 - Fair Division:

Teacher: “At one point Small Number asked his father, ‘How are we going to divide the salmon among our families?’ and his dad answered, ‘We have our ways.’ How do you understand Dad's answer?”

Heidi: “I think that this is what we call Traditional Knowledge, something that Indigenous people have been doing over long period of time.”

Ivan: “That is something that Small Number's dad learned from his dad and his dad learned from his dad.”

Jane: “Is everyone going to get the same number of fish? I think that would be fair.”

Ivan: “I am not sure if that would be fair. What if Small Number's uncle has five children? Then they should get more food.”

Krystal: “Maybe Grandpa is preparing a big feast, so maybe he will get more than others?”

Teacher: “Thank you all. This is a very interesting discussion and, yes, ‘we have our ways’ refers to Traditional Knowledge.”

“And things could get complicated, so the decision about how to divide the harvest must consider all constraints. Let me share with you what I've learned from one Elder¹.”

“The amount of fish one gets depends on how much was harvested. Also, it may be important what kind of fish was harvested, sockeye, chum or coho? The question is if the harvested fish would be for immediate consumption or storage for the winter. Barbecuing means the fish would be consumed within a short period of time. The number of families or community members working together to smoke salmon would determine how much each one (family) gets.”

“So many factors: one family may have dried fish left over and not want as much in this particular harvest. Size of the family participating, there may just be a couple and they would not want as much. All this is done in a very polite way. Processing of the fish is also important in the division of completed food source. For example, fish eggs could be dried and distributed. Personally if I were in the group I would refuse that part because it is now frozen and I do not like frozen eggs.For another example, take the distribution of the fish heads. For this part which is so good, but again dependent on what type of fish. Chum heads are most valued (well me and my family prefer chum heads). Cutting the meat into sections or neck ties also become part of the distribution. Some very traditional people hang the fish backbone because it still has meat. We all seem to work it out somehow.”

Laura: “This is all very interesting, but what does this have to do with mathematics?”

Teacher: “That is an excellent question, Laura!”

“Believe it or not, the problem of fair division is an important mathematical question: How do we divide something so that every person feels they received a fair share? The challenge comes from the fact that different people may feel differently about the same item. Mathematicians are trying to find ways that will guarantee that everyone gets a ‘fair share’ but it might not be the ‘fair share’ they wanted.”

Teacher: ‘Let me give you an example:

Two sisters, Megan and Nancy, just arrived at their uncle's cabin on the island. When they approached the door they saw a handwritten note: ‘Welcome, Megan and Nancy! I am in the village buying groceries. The key is in the big red pot. If you are hungry please eat the fruit that I left for you on the table. Love, Uncle.’

When Megan and Nancy entered the cabin they saw two plates on the table. One plate was full of fresh strawberries and the other was full of yummy looking blueberries.

The sisters biked all the way from the ferry terminal and they were both very hungry. Looking at the two plates on the table they realized that their uncle didn't know that Alice was allergic to strawberries and she was not allowed to eat them. At the same time, blueberries were both Alice and Megan's favourite fruit. How should Alice and Megan divide the fruit that was on the table?’

[Teacher moderates the discussion. “What do you think is a fair thing to do in this situation?” If a student suggests that Alice should get the plate with blueberries and Megan the plate with strawberries, the Teacher should ask: “But blueberries are Megan's favourite fruit, is it fair that she does not get any?” This can be followed by the question: “If Alice were not allergic to strawberries, what would be a fair way to divide the fruit?” or, “If Alice were not allergic to strawberries, what would be a fair way to divide the plate with blueberries?” Or, “If you were Alice, how would you divide the fruit?” Or, “if you were Megan, how would you divide the fruit?” The teacher should lead the discussion to the conclusion that Alice and Megan should each get half of the blueberries and that Megan should eat as many strawberries as she wishes. This exercise might help the teacher to learn something new about their individual students and the class a a whole.]