Adventures of Small Number: Classroom Resources

Paying attention to details - counting

Here is a possible scenario:

Teacher to the class: “Did you like the film? Would you like to see it again?” And later: “Let me ask a few questions about the film.”

The first question should be: “How many animals were in the story?” It is likely that different students will give different answers.

The teacher should invite everyone to answer this question: “Alice, what do you think? How many animals were in the story?” After hearing several different answers, the teacher invites one of the students to list all of the animals: “Bob, would you please list all animals that were mentioned in the story?” While Bob is listing the animals, the teacher counts them aloud and uses their fingers to record the count:

Bob: “Bear...”

Teacher: “One...” and lifts one finger. Regardless of what Bob's answer is, the teacher says to Bob and then to the class: “Thank you, Bob! Do you agree with Bob?” [Teacher moderates the follow up discussion accordingly.]

Teacher to the class: “How many of the animals live in the water? How many of the animals can fly?” [Teacher moderates the follow up discussion accordingly.]

Teacher to the class: “Let me ask you a difficult question. Are you ready?” After waiting for a few moments to get students? attention and to build a bit of suspense, the teacher continues: “How many animal legs did you see in the film?”

This is not an easy question for young or even older students: at each step students are expected to match each animal with the number of its legs and to add that number to the sum established in the previous step. A student may also come up with the correct answer by reasoning in the following way: “There are four animals (bear, wolf, beaver, and frog) with four legs and two animals (eagle and raven) with two legs each so the answer is \(5\times4 = 20\text{.}\)”

The teacher should be prepared to hear a variety of answers. Some students will try to count, some of them will guess the answer, some of them will stay quiet. The teacher should not be surprised if a student offers an odd number as the answer. This could be an opportunity to remind students that the sum of even numbers must be an even number. But, almost certainly, there will be a student who shouts the correct answer: “Twenty!”

After praising those students who came up with the correct answer, the teacher should turn this into a class activity: “Let us do this together. Alice, what was the first animal in the film? How many legs did that animal have?” And so on.

Teacher to the class: “Are you ready for a really, really difficult question?” Again, after waiting for a few moments to get students? attention and to build a bit of suspense, the teacher continues: “What was the oldest animal in the film?”

Here is a possible scenario:

Carol: “The Bear!” (Or some other animal.)

Teacher: “Carol, why do you think that the bear is the oldest?”

Carol: “Because it is the tallest!”

Teacher to the class: “Yes, it is possible that the bear is the oldest among all animals in the film.”

Teacher: (Smiling) “I am the oldest person in our class and I am the tallest. But, think about your favourite soccer team. Is the tallest person in the team at the same time the oldest person?” [Teacher moderates the follow up discussion accordingly.]

Teacher concludes the class discussion by saying: “We actually cannot be sure what is the oldest animal. Sometimes in mathematics, same as in life, there are questions that we cannot answer without additional information.”

Point 2: Paying attention to details - finding differences

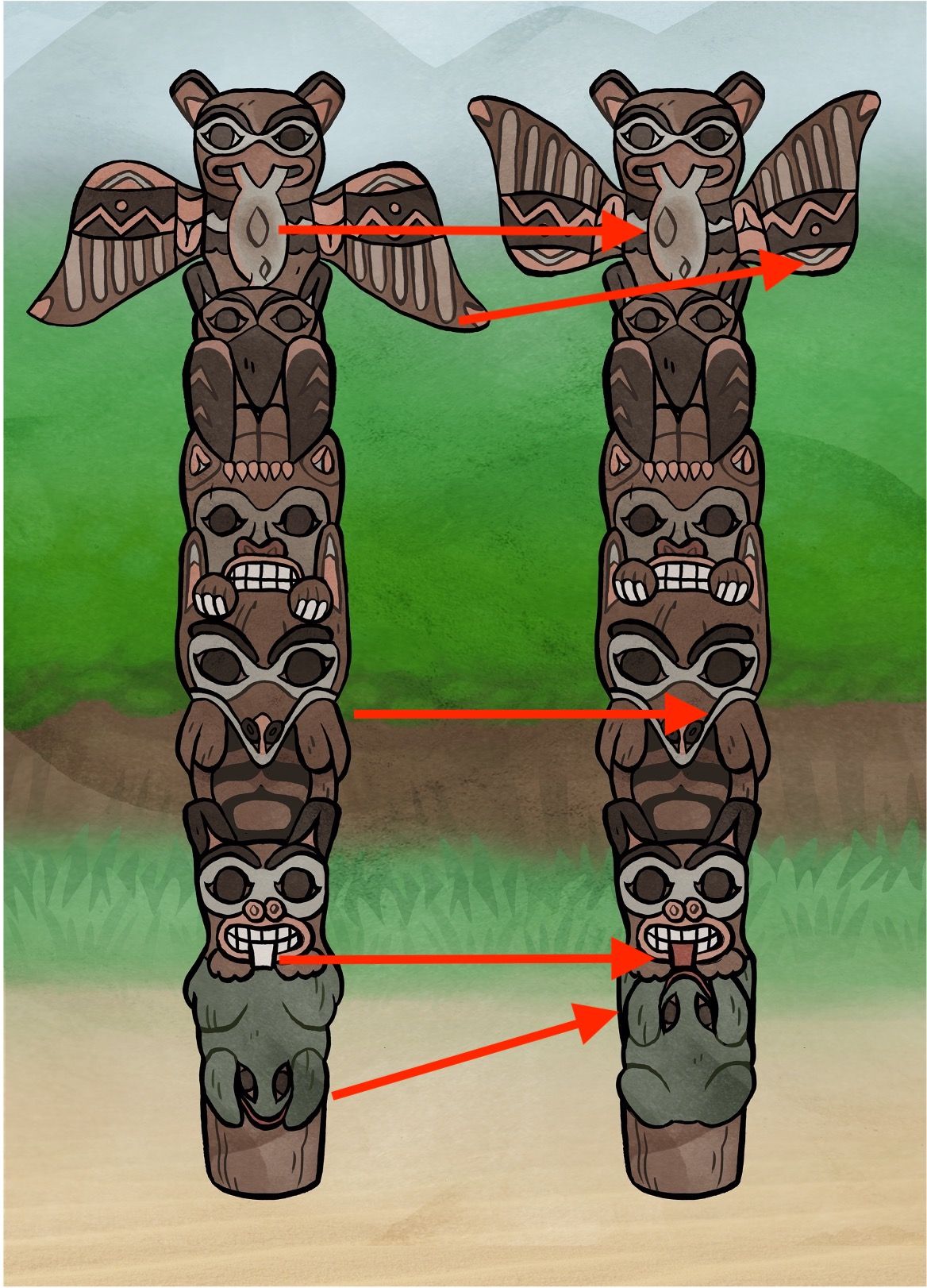
The goal of this activity is to make students aware that in mathematics finding differences in the details between two objects may be important.

Teacher to the class: “Let us look together at this image (figure 7.1.3). Even though at the first glance the two totem poles may look the same, they differ in five details. Can you find them?”

Teacher moderates the discussion. The five differences are presented below (figure 7.1.4):

Point 3: Paying attention to details - ordering

The goal of this activity is to make students aware that it is possible to order the elements of a set in different ways depending on a given rule. The so-called linear ordering, i.e. the ordering in which each element of the set is labeled by a unique natural (ordinal) number \(1, 2, 3,\:...\text{,}\) is quite intuitive and this activity could be an opportunity to communicate with the class its mathematical side. In addition to the fact that there may be more than one linear ordering, this discussion may include the transitivity of an ordering (i.e. if \(A\) comes before \(B\) and \(B\) comes before \(C\) then \(A\) comes before \(C\)) as well as the question of how many linear orderings are possible.

Teacher to the class: “Let us look together at this image”. (figure 7.1.6)

Teacher: “Who is going to tell me the order in which the animals appeared in the film?”

Husein: “The first animal was the salmon, the second was the eagle, the third was the raven, then the bear, the wolf, the beaver, and the frog was the last one.”

Teacher: “Thank you, Husein!” Teacher draws the following table on the board:

Teacher: “But let me ask you if you can come up with some other way to order the animals from the image?”

Ivan: “Maybe we can order them by how big they are?”

Teacher: “That is a great idea, Ivan! Would you like to try?”

Ivan: “The bear is the biggest, then wolf, in this drawing I think that salmon is bigger than the eagle, the eagle is bigger than the beaver; the beaver is bigger than the raven, and the frog is the smallest.”

Teacher: “Thank you, Ivan!” Teacher adds another row to the table:

Teacher: “Any other ideas?”

Jin Sun: “I like frogs and I?d like to see the frog at the first place. So what if we list the smallest animal first?”

Teacher: “Excellent idea, Jin Sun!” Teacher adds another row to the table:

Teacher moderates the follow up discussion, maybe students will come up with another ordering on their own. In the case that they do not, the teacher may suggest: “Do you know what the alphabetical ordering is?”

Suppose that students look puzzled and that Teacher needs to explain. “We have seven animals: salmon, eagle, raven, bear, wolf, beaver, and frog.”

“I am going to look at the first letter of each word: \(\color{red}{S}\text{,}\) \(\color{red}{E}\text{,}\) \(\color{red}{R}\text{,}\) \(\color{red}{B}\text{,}\) \(\color{red}{W}\text{,}\) \(\color{red}{B}\text{,}\) \(\color{red}{F}\text{.}\) Which of these letters comes first in the alphabet?”

Class: “The letter \(B\text{!}\)”

Teacher: “Thank you! I have two letters \(B\text{:}\) \(\color{red}{B}\text{,}\) \(\color{red}{B}\text{.}\) Which letter comes next?”

Class: “The letter \(E\text{.}\)”

Teacher: “Yes!”

Karan: “I know! The next letter is F, and then the letter R, and then the letter S, and the last letter is the letter W.”

Teacher: “Excellent observation, Karan!”

Teacher: “I will list the animals in this alphabetical order, by the first letter. But I have two letters B and I need to decide which animal should be listed first, the bear or the beaver. What do you think?”

It is possible that there will be a student who answers this question correctly. In any case Teacher should state the rule: “This is the rule: if I have two words that begin with the same letter, then I look at the second letter of each word. If those letters are different then I chose one that comes first in the alphabet. If they are equal, I look at the third letter of the each word. Look, we have the words \(\color{red}{bea}\color{green}{r}\) and \(\color{red}{bea}\color{green}{v}er\text{.}\) Which of these two words should come first?”

Lindsay: “The bear, because the letter \(\color{green}{r}\) comes in the alphabet before the letter \(\color{green}{v}\text{!}\)”

Teacher: “You are absolutely right, Lindsay!” Teacher adds another row to the table:

Teacher: “You may wonder why we talk about different ways to order seven animals from the film in a math class. Well, you notice that I used numbers to indicate which animal was the first, the second, and so on by any given rule. For example, by the rule of ‘appearance’ the raven was given the number \(3\) and by the rule of ‘biggest to smallest’ the raven was given the number \(6\text{.}\) Those numbers are also telling us that two animals appeared in the film before the raven and that there were five animals that were bigger than the raven. So, I hope that you agree that using numbers here is useful. And when we talk numbers, we talk mathematics. But these numbers are also kind of different. They are more like stickers that we put on each animal based on the rule that we follow.”

[What happens here is that we use \(1,2,3,\:...\) as ordinal numbers, so saying \(``1 + 1 = 2''\) does not make much sense in this context. Maybe a student will notice this!]

“Can you guess how many lines I need to write down to list all of the different ways to order the seven animals?”

[The number is \(5040\text{.}\) The logic here is the following: for the first place we have \(7\) choices; once the first place is occupied we have \(6\) choices for the second place; when the second place is assigned we are left with \(5\) choices for the third place, and so on. So, the number of all different (linear) orderings of seven objects is \(7\times6\times5\times4\times3\times2\times1 = 5040\text{.}\)]

Mirjana: “One hundred!”

Teacher: “Go up!”

Nancy: “Ten thousand!”

Teacher: “Go down!”

[Teacher may wish to play a few rounds of this guessing game.]

Teacher: “I will need five thousand and forty lines! If we need to write them all down we will probably stay here for a few days! Can you imagine how big this number would be if we had \(10\) animals to list in all possible ways!”

Teacher: “This is why you study mathematics: to learn how to find the number of things that you really cannot or don't have time to count one by one.”

Teacher: “Mathematics helps us to understand what is important and what is not. Let me give you an example. My cousin has three children: Clovie, Justin, and Zack. Justin is older than Zack and Zack is older than Clovie. Who is older, Justin or Clovie?”

Nadia: “That is easy. Justin is older than Clovie! I have two older sisters and I am the youngest in our family.”

Teacher: “Thank you, Nadia! I didn't know that you have two older sisters. Let us play a little game so that you can see that all lines in our table have the same property. Here is the table:”

Teacher: “In one of the lines, the raven comes before the eagle and the eagle comes before the wolf. Which line is this?”

Olga: “I know! The raven must come before both the eagle and the wolf. This happened when we started with the frog, the smallest animal.”

Teacher: “That is a perfect answer, Olga! Thank you!”

Teacher: “So remember, if things are in order, and if one thing, say \(\color{blue}{\blacksquare}\) comes before another thing, say \(\color{red}{\bullet}\text{,}\) and that other thing comes before something else, say \(\color{green}{\blacktriangle}\text{:}\) then \(\color{blue}{\blacksquare}\) comes before \(\color{green}{\blacktriangle}\text{,}\) like this:”

“This is how mathematicians know if some rule will put things in order or not.”

Point 4: Paying attention to details - sorting by a common property and sets with no common elements

The goal of this activity is to provide students with an opportunity to work with sets: Does an element belong to the set determined by a certain property? We can represent a set by using a Venn diagram. When are two sets equal? When is a set a subset of another set? Do two sets have a common element or not? Find the intersection of two or more sets. Be aware of the existence of the empty set. Find the union of two sets.

Teacher to the class: “Let us look together at this scene from the film.” (Figure 7.1.9)

Teacher: “Please help me to complete this table:”

[Teacher moderates the class discussion. Teacher may wish to add more lines to this table. The completed table should look like the table below. While filling up the table, the teacher should intentionally make a couple of mistakes. If students don't react right away, Teacher should invite students to look closer: “Please double check if I made a mistake somewhere.” The point here is to send to students a few important messages: “Everyone makes mistakes. Regardless how confident you are, double check your work. Invite others to check your work - it is always easier to spot mistakes that other people make than your own mistakes.”]

Teacher: “Thank you! Let us see what we've got:”

[Note: The phrase “has \(2\) legs” should actually be “has exactly \(2\) legs”. A student may argue that an animal that has \(4\) legs also qualifies as an animal that has \(2\) legs. The same is true for the line that says “has \(3\) legs”.]

[Next, Teacher wants to make sure that students know how to read the table so they proceed with the following activity. This activity also contributes to building ways of mathematical thinking.]

Teacher: “Let us play a little game. Look at the table and solve this puzzle. I live in water, I have four legs, and I have fur. Who am I?”

Amendeep: “It's the beaver!”

Teacher: “Excellent, Amendeep! How did you find this so quickly?”

[Hopefully, Amandeep will answer that she read this from the table, but it could be that she just independently connected everything in her mind, or maybe she just guessed. In any case, the teacher should point to the relevant cells in the table and state that each cell contains a “\(\color{green}{\checkmark}\)”. Also, the teacher should invite the class to check if there is another animal with the same combination of the “\(\color{green}{\checkmark}\)” answers.]

[Teacher may wish to play more rounds of this game. The following two puzzles underline important mathematical ideas, the existence of an empty set and that if a question has more than one correct answer, all those answers must be listed: “I have three legs. Who am I?” and “I can fly and I have two legs. Who am I?” The first answer is “There is no such animal.” The second answer is “There are two such animals, the eagle and the raven.”]

Teacher: “In mathematics when we say a set we think about a collection of things that is somehow put together. To represent sets we use drawings that we call Venn diagrams. For example, look at the first line of our table:”

“There are two animals that can fly, the eagle and the raven. I am going to draw them and then put this closed shape around them.”

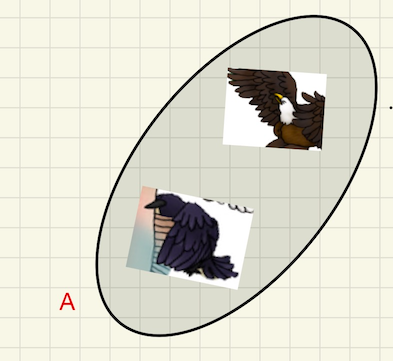
“This is a Venn diagram of the set of all animals in the film that can fly. The diagram shows that the eagle and the raven belong to this set and that, for example the bear does not. I'll write the letter ‘\(A\)’ beside the Venn Diagram so that I know this is the set that is matched with the line ‘\(A\)’ in our table.”

“Is this OK? Did you understand how I got the Venn diagram? Do you have any questions? Are you ready to try to draw the diagram for the line B?”

Brenden: “I did it already! This is a Venn diagram of the set of all animals that live in water.”

Teacher: “That is excellent work, Brenden!”

[And so on. Observe that the set \(F\) is an empty set - a set with no elements. The outcome should be seven Venn diagrams like in Figure 7.1.10.]

Teacher: “Learning about sets is an important part of learning mathematics. Let us explore together some of the properties of sets.”

Teacher: “If you look at all Venn diagrams that we have drawn, one of them looks kind of special. What do you think?”

Cindy: “Yes, there is a Venn diagram with nothing in it. That is weird, I think.”

Teacher: “I agree, Cindy. That is kind of weird. We say that a set with no elements is an empty set.”

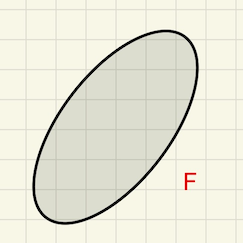
To the class: “Can you think about another example of an empty set?”

Teacher: “Now, let us look at these two sets. What do you notice?”

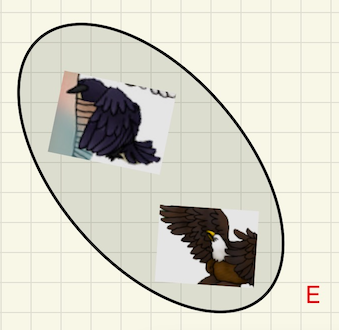
Dexter: “I see that the raven and the eagle are in both sets.”

Teacher: “That is a very good observation, Dexter. Do you see any other elements in either of the sets?”

Dexter: “No.”

Teacher: “Thanks, Dexter.” To the class, “When we have something like this, that two sets have the same elements, we say that those two sets are equal.”

“What is really important here is to notice that these two Venn diagrams kind of look different, one is slanted to the left and the other is slanted to the right. In one of them the raven is above the eagle and in the other the eagle is above the raven. Even more, those two Venn diagrams represent sets obtained by two different rules, for one the rule was ‘I can fly’ and for the other the rule was ‘I have two legs.’ But all those differences do not matter, these two sets have the same elements, the raven and the eagle, and for us they are equal.”

Teacher: [After a short pause.] “This is another reason why you learn mathematics. When we think about something it is always useful to distinguish what is more important from what is less important.”

Teacher: “Now, let us look at these two sets. What do you notice?”

Fok: “I see that the bear, the beaver, and the wolf are in both sets, but that the frog is only in one of them!”

Teacher: “Wow, Fok, that was very well said! I will say the same thing, just a bit differently: all elements of the set \(C\) are also elements of the set \(G\text{,}\) but the set \(G\) has an element that is not in \(C\text{.}\) Look!”

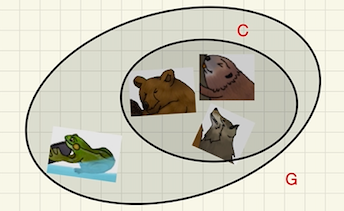
Teacher: “When something like this happens, we say that one set is a subset of the other set. Here we have that the set \(C\) is a subset of the set \(G\text{.}\) Can you say the word ‘subset’?”

Fok: “So a subset is a smaller set that is kind of part of the bigger set?”

Teacher: “Exactly, Fok. Look at these three sets in Figure 7.1.11. Is the set \(D\) a subset of the set \(B\text{?}\) Is the set \(B\) a subset of the set \(G\text{?}\) Is the set \(G\) a subset of the set \(B\text{?}\)”

Fok: “I think that the set \(D\) is a subset of the set \(B\) because the salmon is in both sets and there is nothing else in the set \(D\text{.}\)”

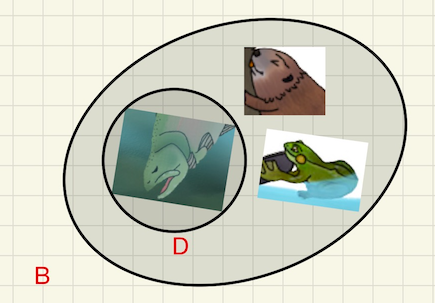
Teacher: “What about sets \(B\) and \(G\text{?}\)”

Fok: “\(B\) is not a subset of \(G\) because the salmon is in the set \(B\) but is not in the set \(G\text{.}\) The set \(G\) is not a subset of the set \(B\) because the bear is in the set \(G\) but is not in the set \(B\text{.}\)”

Teacher: “Fok, you talk like a real mathematician. Excellent!”

“Fok is right, the set \(B\) is not a subset of the set \(G\) and the set \(G\) is not a subset of the set \(B\text{.}\) But, have you noticed that \(B\) and \(G\) have two elements, the beaver and the frog, in common?”

“We say that the set of the common elements of two sets is their intersection. The symbol for the operation of finding the intersection of two sets is this: [writes on the board] \(\cap\).”

Gabriela: “That symbol looks like an upside down letter \(U\text{!}\)”

Teacher: “I thought the same when I saw it for the first time.”

“Gabriela, what if you help me to draw the intersection of the sets \(B\) and \(G\text{?}\)”

Teacher: “There is one more thing that I'd like to share with you about sets. What if we are asked to draw a Venn diagram of the set of animals from the film that have at most two legs.”

Teacher: “But, let me ask you, how do you understand the phrase at most two?”

Helen: “That means one or two, I think.”

Teacher: “That is almost right, Helen. But what about the number zero? What do you think?”

Helen: “Yes, at most two means numbers that are not bigger than two, so zero, one or two!”

Teacher: “Very good, Helen. So which animals belong the set of animals from the film that have at most two legs?”

Helen: “The salmon has no legs, so it is in this set. There is no animal with one leg. The raven and the eagle have two legs. The salmon, the raven, and the eagle!”

Teacher: “Thank you, Helen!” [To the class:] “Remember what Helen said, at most two means not bigger than two. If you look a bit closer at the Venn diagram of the set of all animals with at most two legs you can see that what we actually did was to join the set \(D\) and the set \(A\text{.}\) This new set is called the union of \(D\) and \(A\text{.}\) We use the symbol \(\cup\) for this operation.”

“You think about union of two sets as putting all elements from the two sets together.”

Teacher: “What if we are asked to draw a Venn diagram of the set of animals from the film that have at least two legs.”

Teacher: “But, let me ask you, how do you understand the phrase at least two?”

Karim: “That means two or more, I think.”

Teacher: “You are right, Karim. So we should look for which animals here?”

Karim: “I think every animal except the salmon!”

Teacher: “Thank you, Karim!” [To the class:] “Remember what Karim said, at least two means two or more. If you look a bit closer at the Venn diagram of the set of all animals with at least two legs you can see that this is the union of the \(A\) and the set \(G\text{.}\)”

“Remember, the union of two sets contains all elements from both sets.”

Point 5: What makes things big or small?

Teacher to the class: “Let us look together at this scene from the film.” (Figure 7.1.13.)

Teacher makes sure that each student has had a chance to see the image.

Teacher to the class: “Which animal in the picture is the biggest?” [After waiting for a moment:] “Which animal is the smallest?”

A few hands go up. The teacher chooses Dave, for example.

Dave: “The bear is the biggest and the frog is the smallest animal in the picture.”

Teacher: “Thank you, Dave. I agree with you.” To the class: “Yes, the bear is a big animal! But can you think about an animal that is bigger than the bear? Or about an animal that is smaller than a frog?”

[Teacher moderates discussion with the goal that students, possibly with Teacher's help, list a few animals (like an elephant, a giraffe, or a whale) that are bigger than the bear and a few animals (like a humming bird, a fly, or an ant) that are smaller than the frog.]

Teacher displays on the screen the image of an elephant and a bear.

Teacher: “Comparing with an elephant, a bear looks kind of small. And, believe it or not, the Atlantic blue whale may weigh as much as 33 elephants together. So comparing with a whale an elephant looks very small and a bear looks tiny.” (See World Wild Life)

Next Teacher displays on the screen the image of a frog, a fly, and an ant.

Teacher: “When you compare it with a fly or an ant, this frog looks like a giant! Do you agree?”

Teacher continues: “Later in school you will learn that there are living organisms that are so small that they can be seen only through a microscope. So, for those organisms, an ant is a giant! Do you know what a microscope is?”

Teacher invites students to find their own examples: “Can you think about something that is small comparing with something else but it is very big if you compare it with another thing?”

Teacher moderates discussion. Here are a few possible answers:

Erin: “I know! If I stand in the front of a tall building and hold a lego piece in my hand!”

Fayza: “I am thinking, our city is a small part of the whole world, and our classroom is a very small part of our city and my desk is a small part of the classroom and my pencil occupies only a very small part of the desk surface.”

Gabor: “If I run on a sandy beach, my footprint looks tiny, but each grain of sand under my foot is much much smaller.”

Helen: “The number one thousand is ten times bigger than the number one hundred and the number one hundred is hundred times bigger than the number 1.”

Teacher: “So, what do you think that makes things big or small?”

[Teacher moderates discussion leading students to conclude that something is big or small only in comparison with other objects or beings. Teacher may wish to use Fayza's example to demonstrate the transitivity of a linear order relation, i.e., if \(a\) is less than \(b\) and \(b\) is less than \(c\text{,}\) then \(a\) is less than \(c\text{.}\)]

Point 6: How does change happen?

Teacher: “How do you understand the word change? What does it mean that something has changed?”

Rebekah: “That means that something looks different than before. Like when my dad shaved his moustache.” [Change by removing.]

Brenda: “Maybe it could be the same thing, just in a different place. Like when I put my phone from my pocket on my desk.” [Change by repositioning.]

Candice: “Or maybe when we replace one thing by another. Like when I buy new shoes.” [Change by replacing.]

Dino: “Each time when I visit my grandma she tells me that I have grown so much. So, my height is changing.” [Change as a function of time.]

[Teacher moderates discussion. Teacher may wish to write some of the students? ideas on the board. Students should be encouraged to give as many examples as possible with the idea that they realize that change is present in the world around them.]

Teacher: “That is great, everyone! Yes, we are changing and the world around us is changing in many ways. But, can you think about something that is changing all the time?”

Emilia: “I know! The time on the clock is changing all the time! Look!” [Points to the clock on the wall.]

Fan: “Also, the weather is changing all the time!” [Points to the window.]

Teacher: “Those are two great examples!”

Teacher: “What do you think, why it is important that we know what the time is at a certain moment?”

Gaven: “So that we know when is time for the recess.”

Teacher: “You are absolutely right, Gaven! We keep track of time because that tells us when we need to do certain things. At 9:00 I will start our first class, we have a recess at 10:25, and so on. So, time changes and we change what we do accordingly.”

Teacher: “And you are right, the weather is always changing. It is important for so many aspects of our daily lives to know what kind of weather change is coming.” [To the class:] “Can you think about some examples when it is important to know what the weather will be tomorrow?”

Harleen: “If my mom knows that it will rain, she wants me to wear my rain jacket when I go to school.”

Karl: “Last year my family was planning to visit my grandparents. My mom got an email that our flight was cancelled because of a coming wind storm. We went to the airport the following day.”

Teacher: “Thanks, Harleen and Karl. Those are very good examples. I'll give you a couple more examples that show that everyone's life is affected by the weather changes. For people who manage the water supply it is important to know if there will be enough rain and snow to fill up all reservoirs. For people who manage roads it is important to know if a snow storm is coming so that they can get ready, and so on.”

“Maybe you don't know that mathematics is the main tool in predicting how the weather will change. Maybe you've heard the word calculus? This is an area of mathematics that studies how things are changing. Some of you will learn calculus in high school or university.”

Teacher: “But let us go back to our film. Did you notice any changes in the film?”

Moe: “The number of animals was changing all the time. And each time the salmon will get a little bit closer to the shore.”

Noreen: “The height of animals was changing. The animals were getting smaller.”

Orestes: “At the end all animals transformed to carvings on the totem pole.”

Teacher: “Thank you! Have you noticed that Moe, Noreen, and Orestes used mathematical words, like number of, all the time, a little bit closer to, the height of, getting smaller, and transformed to, to describe the change?”

Point 7: When does a small change make a big difference?

Teacher: “Can you think about an example when a small change made a big difference?”

Peter: “When I visited my grandpa in hospital, he asked me to raise his pillow a little bit. When I did it, he said that made a big difference and that he was much more comfortable.”

Nikola: “If I put just a little bit of salt in my soup, it becomes much tastier.”

[Teacher moderates the discussion with the goal that students observe that a small change can cause a big change.]

Teacher: “Before we go back to the question at the end of the film, I'd like to show you several photos that I made yesterday evening in my kitchen.”

Teacher: “You see, in the first picture I have five glasses of different sizes full of tea and an empty measuring cup. In the second picture, I poured tea from the biggest glass into the measuring cup.”

Teacher: “In the next two pictures you see what happened when I poured tea from the second and the third glass into the measuring cup. Observe that the measuring cap looks almost full of tea.”

Teacher: “As you can see, I was able to pour tea from the next glass into the cup. But then my cat Daisy came to the kitchen to remind me that was time for her dinner. I never tried to pour tea from the last glass into the cup. What do you think that would happen if I emptied the smallest glass into the cup?”

Joanna: “I think that there was enough room in the cup that you could pour tea from the last glass. That glass looks very small.”

Ben: “My uncle has a cat.”

Miranda: “I think that if you poured tea from the last glass it would spill over. That glass looks very small but the cup looks already quite full of tea.”

Justin: “I agree with Miranda. I think that Daisy saved you so that you didn't need to wipe tea from your counter.”

Teacher: “Well, we will never know. I agree with Joanna that the last glass was very small, but I also agree with Miranda that the cup looks almost full. I guess I should thank Daisy…”

Teacher: “Let me remind you about the question at the end of the film: Why did the eagle, the raven, the bear, the wolf, and the beaver need help from a little frog to pull the salmon on to the shore?”

Teacher: “Do you understand the question? What do you think?”

[Maybe students will start sharing their ideas right away. If not, Teacher should encourage them by asking: “Do you think that the photos of five glasses and a cup from my kitchen had something to do with this question? Is filling the cup with tea something similar to putting strengths of animals together to heave the salmon on to the shore?” ]

Teacher moderates discussion leading the class to conclude that, by working together as a group, the animals accumulate their individual strengths and gain enough power to pull the salmon on to the shore. Also, Teacher should point out that similar to the previous examples, this is another case where a small change caused a big change.

Teacher: “Very good! Thank you all! Can you remember a time when you needed help from some friends to finish something you were working on? Has your dad or mom ever asked you to help them with something? Have you ever gone fishing? If you have, what was it like trying to catch a fish?”

Ask students to search internet for “mathematics of change” and to report what they find.

Here are some possible findings:

• “Calculus is the mathematics of change and motion”

• “Calculus can be defined as the study of the rate of change.”

Follow up by saying that the word ‘calculus’ comes from Latin meaning ‘small stone’.

The concept of getting closer and closer and closer

Teacher: “Look at the following list of fractions. Can you recognize the pattern? How does each fraction on the list relate to the one before it”

Aaron: “It looks like that each fraction has a denominator that is two times bigger than the denominator of the previous fraction.”

Teacher: “That is a very good observation, Aaron! Please come to the board and write these fractions in a way that everyone can see the pattern. Also please extend the pattern with a couple of fractions that come next.”

Aaron comes to the board and writes:

Teacher: “Thank you, Aaron!” To the class: “Do you see the pattern? Which fraction comes next?”

Branka: “One over two times one hundred and twenty-eight! That is the same as one over two hundred fifty-six.”

Teacher: “You are absolutely right, Branka!”

To the class: “You remember that we multiply fractions by multiplying the numerator by the numerator and the denominator by the denominator. Right? So I am going to rewrite our pattern in this way:”

Teacher, waiting for a moment before asking: “How would you describe our pattern now?”

Cedric: “Each fraction is one-half of the previous fraction!”

Teacher: “That is a great answer, Cedric! So we make one-half of what we had before. Do you agree that this fractions are becoming smaller and smaller? Already the number \(\frac{1}{256}\) seems quite small. Imagine that you share one pizza with 256 friends and that everyone gets a piece of the same size!”

Teacher: “But, let us practice addition of fractions. Please add these fractions:”

1. \(\displaystyle \frac{1}{2}+\frac{1}{4}= \enspace?\)
2. \(\displaystyle \frac{1}{2}+\frac{1}{4}+\frac{1}{8}= \enspace?\)
3. \(\displaystyle \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}= \enspace?\)
4. \(\displaystyle \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}= \enspace?\)

Teacher walks around and engages with students as appropriate. After some time, teacher invites students to share their answers:

1. \(\displaystyle \frac{1}{2}+\frac{1}{4}= \color{red}{\frac{3}{4}}\)
2. \(\displaystyle \frac{1}{2}+\frac{1}{4}+\frac{1}{8}= \color{red}{\frac{7}{8}}\)
3. \(\displaystyle \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}= \color{red}{\frac{15}{16}}\)
4. \(\displaystyle \frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}= \color{red}{\frac{31}{32}}\)

Teacher: “Do you agree with these answers?” Teacher pauses before continuing: “Please listen carefully because I am going to ask you a strange question.” After a short pause: “Do these answers look right to you?”

Donna: “What do you mean by ‘look right’?”

Teacher: “Thanks, Donna. That is a fair question. I was wondering if you can notice a pattern that these answers follow?”

Donna: “Oh, I see what you mean. Yes, I see the pattern: the numerator of each answer is one less than its denominator.”

Teacher: “Great! So Donna, what would be the answer in the next line?”

Donna: “Sixty-three over sixty-four?”

Teacher: “Excellent answer, Donna! You've just made my day!” To the class: “But what if I write those answers in a different way:”

Teacher: “This is something that you will study in more advanced math classes, but I would like you to notice all of our answers are smaller than the number 1. If we continue with this pattern, our answer will be always less than 1 but by something very very small like \(\frac{1}{256} = 0.00390625\) or \(\frac{1}{512} = 0.001953125\text{.}\) This is where mathematics becomes really interesting! We think about the difference between two numbers that can be as small as we wish!”

Teacher, after moderating discussion and answering students? questions: “But let me ask you this. What would happen if I add all of the fractions from our initial list:”

Esther: “That does not make sense. Even a computer cannot add numbers forever.”

Teacher: “Esther, you make me feel so proud to be your teacher! Yes, you said it as it is: even a computer cannot add numbers forever. It took mathematicians a very long time to make sense of the notion of an infinite sum. You will learn all about it in a calculus class.”

Teacher: “My question is more about what your intuition is: what would happen if I continue taking away from the number 1 a number that is getting smaller and smaller?”

Esther:. “You will get closer and closer to 1?”

Teacher: “Yes! And now I would like to show you something really cool.”

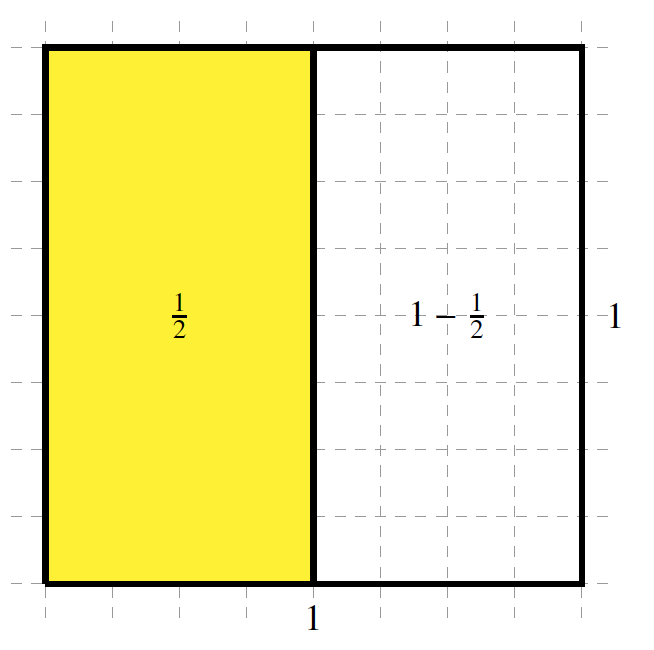
“What you see here is a \(1\times1\) square. In the second image, I covered half of the square by a yellow rectangle. Observe that \(1-\frac{1}{2}\) of the original square is not covered.”

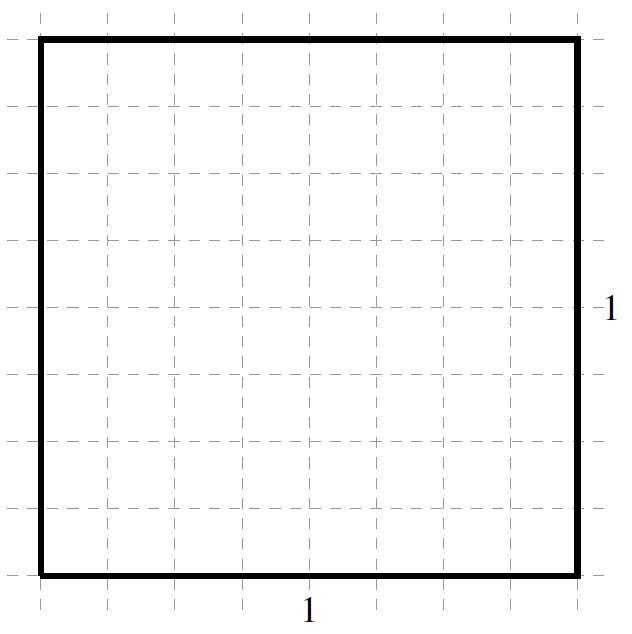
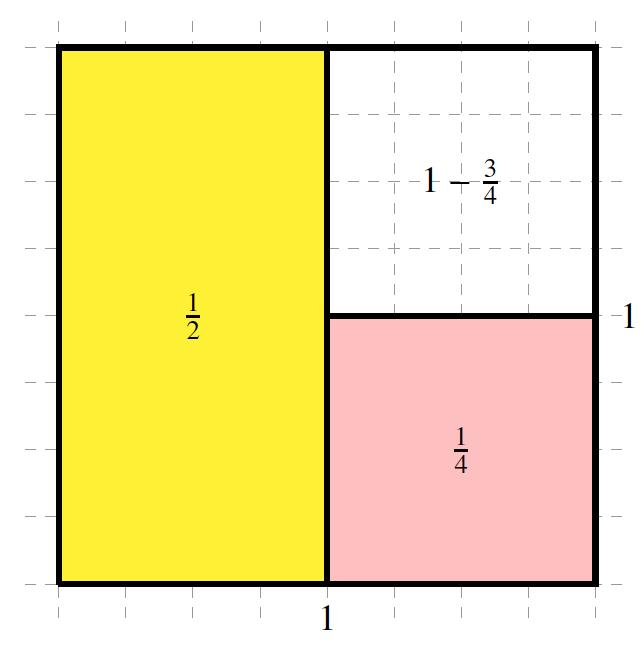
“Next I will cover one-half of the uncovered area of the original square by an orange square. The area of that square is \(\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}\text{.}\) Observe that \(1-\frac{3}{4}=\frac{1}{4}\) of the original square is still not covered.”

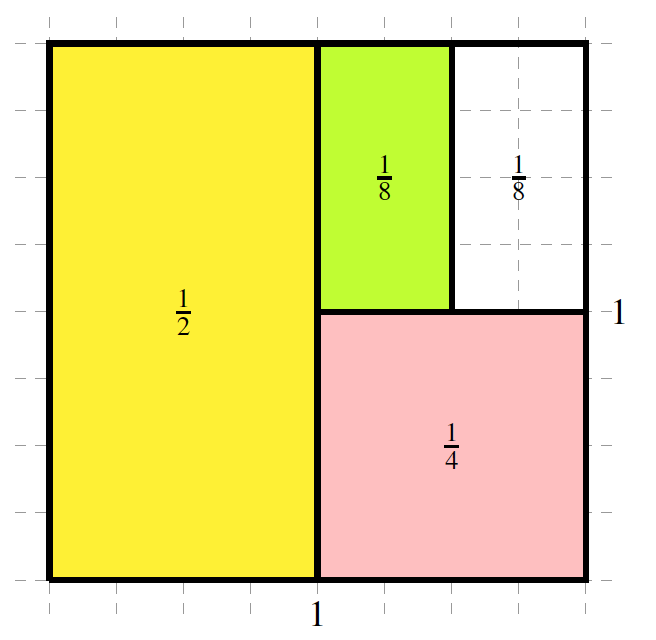
“Next I will cover one-half of the uncovered area of the original square by a green rectangle. The area of that rectangle is \(\frac{1}{2}\times\frac{1}{4}=\frac{1}{8}\text{.}\) Observe that \(1-\frac{7}{8}=\frac{1}{8}\) of the original square is still not covered.”

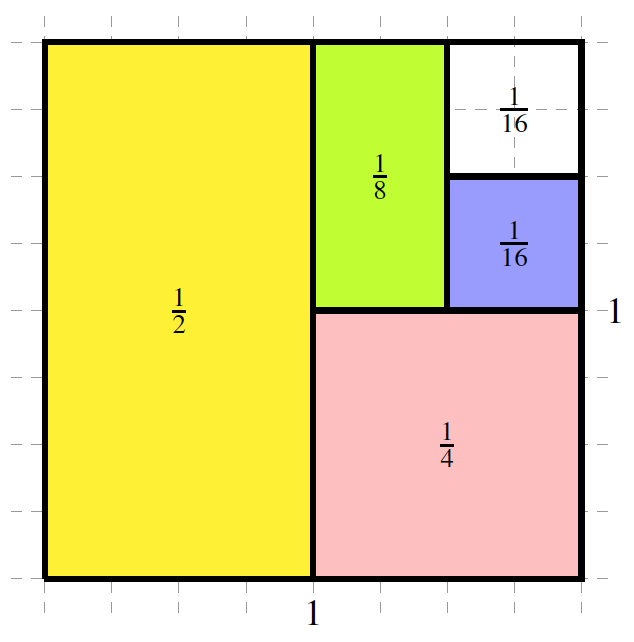
“Next I will cover one-half of the uncovered area of the original square by a blue square. The area of that square is \(\frac{1}{2}\times\frac{1}{8}=\frac{1}{16}\text{.}\) Observe that \(1-\frac{15}{16}=\frac{1}{16}\) of the original square is still not covered.”

“Next I will cover one-half of the uncovered area of the original square by a red rectangle. The area of that rectangle is \(\frac{1}{2}\times\frac{1}{16}=\frac{1}{32}\text{.}\) Observe that \(1-\frac{31}{32}=\frac{1}{32}\) of the original square is still not covered.”

“Next I will cover one-half of the uncovered area of the original square by a brown square. The area of that square is \(\frac{1}{2}\times\frac{1}{32}=\frac{1}{64}\text{.}\) Observe that \(1-\frac{63}{64}=\frac{1}{164}\) of the original square is still not covered.”

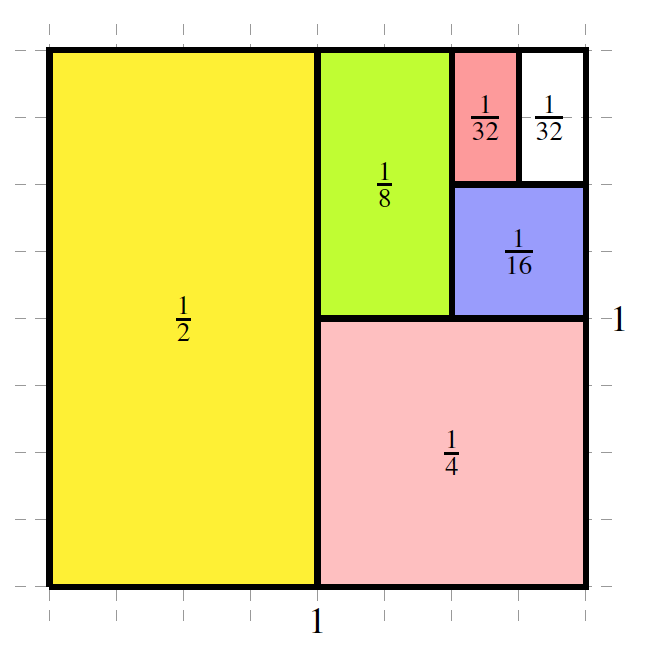
“What do you think would happen if I continue covering one-half of the uncovered area? Would I be able to cover the whole original square at some point?”

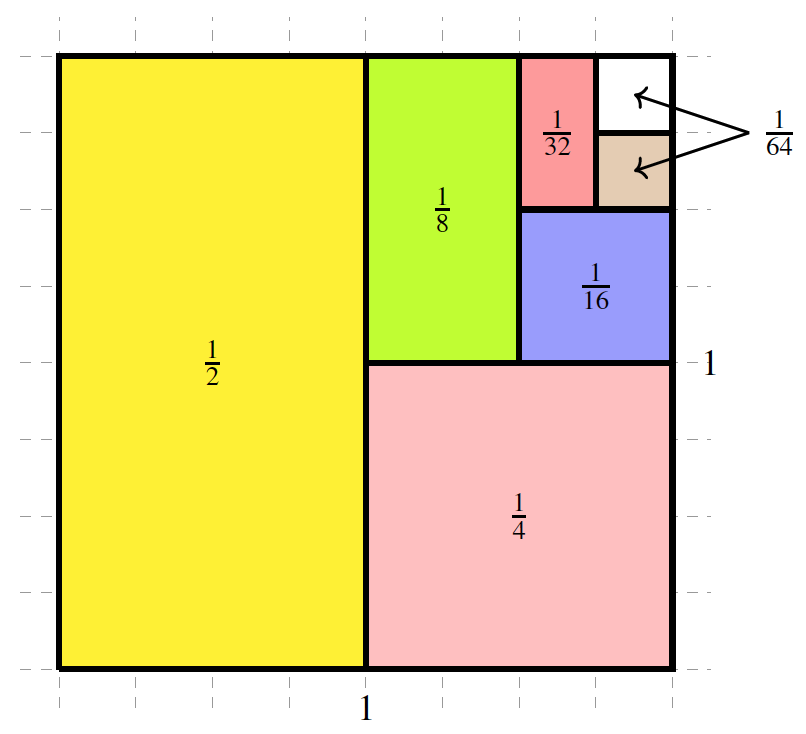
Teacher moderates the discussion with the goal that students conclude that in each step some area of the original square will be not covered. At the same time, with each step the uncovered part of the square would become smaller and smaller and smaller.

Using what we know to find what we don't know and the concept of approximation

Teacher: “Your class is tasked to draw and paint the school's logo on the outside wall of the gym. Since the wall was exposed to rain for many years, you need to seal part of the wall in the following shape:”

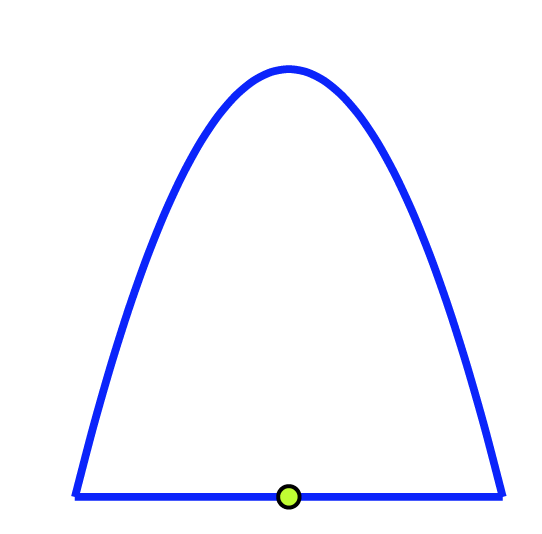
“The bottom, straight part of the arch is 4 metres long, and the height of the arch in the middle is 4 metres. To find the height of the arch at any other point along the bottom, we calculate how far away from the middle we are. We multiply this distance by itself, then subtract the result from 4. That is how high the arch is.”

Teacher: “Do you understand the rule how the height of the arch is calculated? What if we try to complete this table.”

Dexter: “Does it matter in which direction we go from the middle point, left or right?”

Teacher: “An excellent question, Dexter! Thank you! No, it does not matter if you are 0.5 metres to the left or to the right form the middle point.”

Erica: “May I do it on the board?” A little bit later: “If the distance is \(0.5\) metres then the height is \(4 - 0.5\times0.5 = 4-0.25 = 3.75\) meters. If the distance is \(1.5\) then the height is \(4 - 1.5\times1.5 = 4 - 2.25 = 1.75\text{.}\) If the distance is \(2\) then the height is \(4 - 2\times2 = 4 - 4 = 0\text{.}\)”

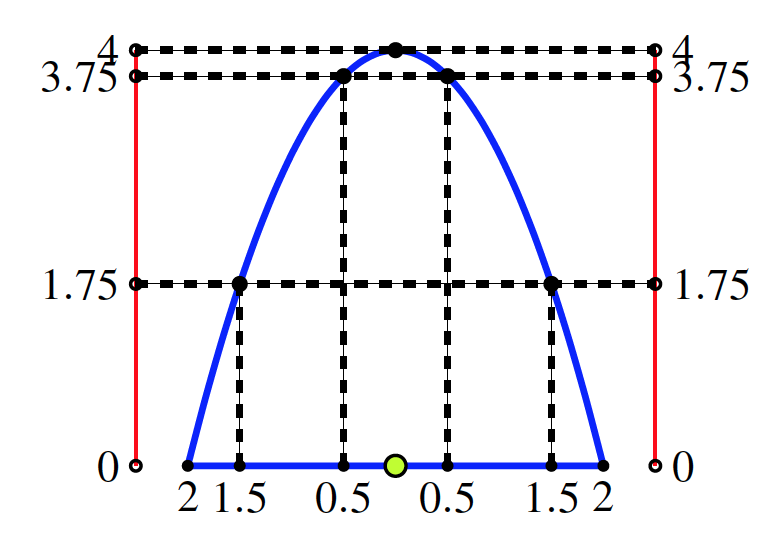
“So the table looks like this:”

Teacher: “Excellent work, Erica!” To the class: “Do you have any questions for Erica?” After a pause. “So your job is to seal this particular piece of wall that is bounded by the arch and the line segment. At the meeting with Mr. Ramsey, the school principal, you are told that the budget for the project is very tight, so that you have to buy only supplies that are really necessary. ‘Don?t waste any money’, Mr. Ramsey repeated several times.”

Teacher continues: “At the group meeting, you are discussing how much sealant you need to buy. ‘What is the area that we need to seal?’ asks one your friends. ‘I don't know’, you answer. ‘But I have an idea how we can estimate the area’. You draw the arc on a piece of paper.”

“To estimate the area of the arch shape, we can put a bunch of small rectangles over it, and add the areas of the rectangles. For example, we can use four rectangles, all with the same width (one metre) and different heights.”

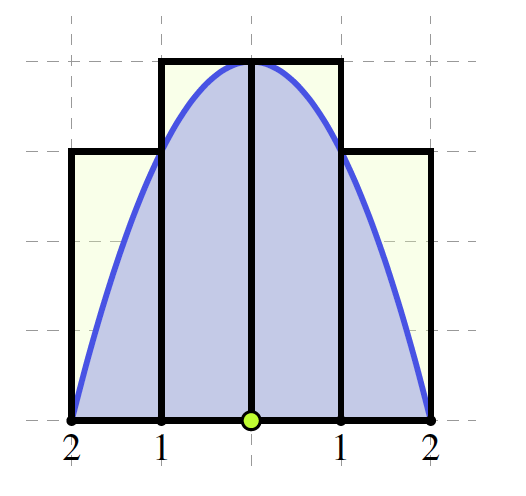
Teacher: “Here are a few questions for you:”

1. What is the height of each of the four rectangles?
2. What is the area of each of the four rectangles?
3. What is the total area of the four rectangles?
4. Is this total area an over-estimate or under-estimate for the area of the arch shape?

“Don't hurry, take your time to find all answers. Compare your answers with the classmate who is closest to you. Let me know when you are ready to share your answers.”

After some time…

Polly and Benjamin: “We worked together and here are our answers:”

1. The outside rectangles have the same height \(4 - 1 = 3\) metres. The height of both inside rectangles is \(4\text{.}\)

2. The outside rectangles have the same area \(1\times3\) square metres. The inside rectangles have the area \(1\times4 = 4\) square metres.

3. The total area of all four rectangles is \(2\times3 + 2\times4 = 14\) square metres.

4. From the picture we see that the area of the four rectangles together is bigger than the area under the arc. So it is an over-estimate, The area under the arc is less than \(14\) square metres.

Teacher: “Excellent work, Polly and Benjamin!” To the class: “Do you agree with Polly and Benjamin?s answers? Do you have any questions?”

Teacher: “When we shrink the width of each rectangle, and use more rectangles, we can get closer to the area of the arch. Suppose we use eight rectangles, all of width \(0.5\) metres like this:”

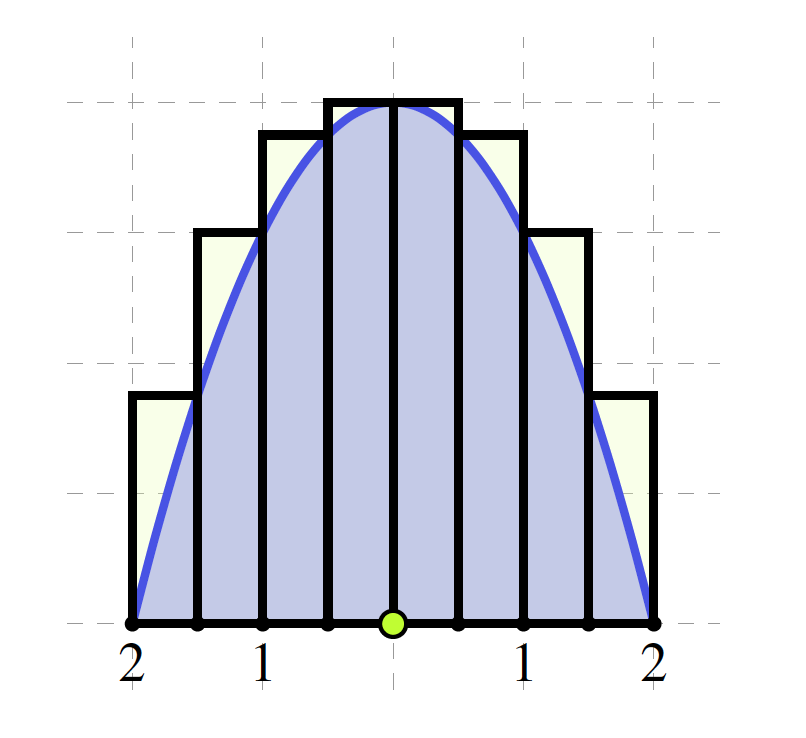
Teacher: “I have two questions for you:”

1. What is the height and area of each rectangle here?
2. What is the total area of the eight rectangles? Is this total area an over-estimate or under-estimate for the area of the arch shape?

“Please work on these two questions and let me know when you are ready to share your answers.”

After some time...

Mahsa and Felix: “We are ready:”

• Our strategy was to look just at the right hand side of the picture. Because of the line symmetry, each rectangle on the left hand side has a matching rectangle on the right hand side. We made this table:

• The total area of the eight rectangles is

  \begin{equation*} 2\times(2 + 1.875 + 1.5 + 0.875) = 2\times6.25 = 12.5 m^2 \end{equation*}

  From the picture we see that the area of the eight rectangles together is bigger than the area under the arc. So it is an over-estimate. The area under the arc is less than \(12.5\) square metres.

Teacher: “Great work, Mahsa and Felix!” To the class: “So what is the amount of sealer that you need to buy to cover the area under the arc and not have to much waste?”

Jasmin: “We need enough sealer to cover an area of about \(12.5\) square metres.”

Teacher: “Thanks, Jasmin. Later in calculus you will learn that the exact area under the arc is \(12\) square metres. So you will not have much sealer left.”